El estudio del campo eléctrico es de mucha importancia cuando se encaran los problemas de alta tensión, la mayoría de los fenómenos de interés están muy ligados al campo eléctrico.

Repasemos como se determina el campo eléctrico, entre dos cargas eléctricas se presenta una fuerza figura 4.1:

siendo:

F: fuerza en (N)

r₁: vector unitario (versor) en dirección de la recta que une las cargas, y que da sentido a la fuerza

Q₁, Q₂: cargas eléctricas puntuales (Culomb)

e ₀: permitividad del vacío = 8.859 ´ 10^-12 (F/m)

r: distancia entre las cargas (m)

Si la carga Q₂ es una pequeña carga de prueba positiva, se define la intensidad del campo eléctrico (en Newton / Culomb = Volt / m):

Si la carga Q₁ es positiva, y como la carga de prueba también lo es, las cargas se repelen, la fuerza es en la dirección de la recta que une las cargas, en el sentido de alejarlas, y este es el sentido del campo también.

Si hay varias cargas, consideradas individualmente en un punto nos dan varios (vectores de) campos, el campo total resultante puede obtenerse por suma vectorial de los campos componentes individuales en cada punto, este es el llamado principio de superposición figura 4.2.

En esta forma puede resolverse el campo entre dos esferas (con cargas de distinto signo), la primera aproximación es suponer que las cargas son puntuales, en el centro de las esferas.

Las superficies equipotenciales son esféricas, sus centros están ubicados sobre la recta de simetría, un par de estas superficies puede representar las esferas reales, al hacer esto se nota que las cargas puntuales usadas para calcular, no son concéntricas a estas esferas.

El espinterómetro a esferas, fue utilizado durante mucho tiempo como instrumento de determinación de la tensión.

Mientras la distancia entre las superficies de las esferas es del orden del diámetro, el campo en la proximidad del eje (que une los centros) es sensiblemente uniforme, cuando el campo alcanza el valor critico se produce la descarga. Para cada valor de distancia entre las superficies de las esferas, se produce la descarga para un valor determinado de tensión aplicada, se mide la distancia entre esferas, y en una tabla se determina la tensión.

Obsérvese el campo entre dos esferas, el campo es simétrico respecto del plano de simetría de las cargas, una mitad del campo espacial es imagen especular de la otra mitad, de aquí comienza a intuirse el método de las imágenes.

El problema de un conductor cualquiera, y un plano conductor infinito, se puede resolver como dos conductores uno imagen del otro (suponiendo que el plano es un espejo).

Físicamente la superficie de reflexión se comporta como una pared metálica (en la cual las líneas de campo son normales).

El método puede ser usado para varias cargas próximas a una pared metálica o al suelo conductor (simplemente de elevada conductividad respecto del espacio dieléctrico).

Si se tiene el suelo y una pared se tienen dos superficies de reflexión normales entre si, habrá dos imágenes (de reflexión en el suelo y en la pared) y otra imagen (de segunda reflexión).

Si la carga esta entre dos paredes paralelas entonces las imágenes son múltiples (en teoría infinitas imágenes como cuando uno se observa entre dos espejos paralelos).

Este método también es válido para superficies curvas, como un conductor dentro de un tubo metálico excéntrico (problema de los conductores dentro de un cable con una única pantalla), o al plantear el campo en el espacio dieléctrico entre dos esferas (espinterómetro de esferas).

Al determinar el campo eléctrico alrededor de un conductor cualquiera, la tierra actúa como superficie especular, y por lo tanto podemos resolver el problema considerando el conductor y su imagen.

Si próximo al conductor se encuentra una pared (conductora) en ella se producirá otra imagen, como visto en el punto anterior.

Uno o más electrodos, encerrados dentro de una sala se resuelven por el método de las imágenes, reemplazando cada pared por las correspondientes imágenes.

El número de imágenes que se debe considerar al tener dos paredes paralelas es infinito, pero es suficiente con considerar un número finito, que no es necesario sea demasiado elevado (4 imágenes parece generalmente aceptable).

Esta simulación corresponde a una sala de ensayos con electrodos en su interior y con paredes techo y piso metálicos, un paralelepipedo.

Dentro de un medio el campo es continuo, de un punto a otro vecino cambia solo infinitesimalmente, en la frontera, límite del medio, el cambio puede ser abrupto (tanto en magnitud como dirección).

Conviene observar el campo en la frontera a través de sus componentes normal y tangencial.

El campo tangencial en la frontera conductor dieléctrico es nulo (efectivamente, el campo es normal al conductor).

Para determinar el campo alrededor de los conductores es necesario saber como se distribuyen las cargas, al determinar el campo en la frontera se obtiene la distribución de cargas.

Cuando se plantean problemas de campo, se tiene una ecuación diferencial valida dentro del área de interés del problema (dominio).

Además se presentan condiciones de borde (frontera, en los limites del área en estudio), estas pueden imponer el valor de la función (solución) en dichos puntos, por ejemplo se busca el potencial en un área, y se conoce el potencial en ciertos puntos, esta condición se la llama de Dirichlet.

La condición de Neumann impone el valor de la derivada (de la solución) en algunos puntos frontera, por ejemplo si dentro del área se tiene un círculo (objeto en general) metálico, la derivada del potencial es normal a dicha frontera.

También se pueden presentar condiciones de tipo mixto, que relacionan el valor de la función y su derivada, en la frontera.

Observemos figura 4.3 una carga lineal indefinida de densidad lineal r _L, pensemos se trata de cargas r _L.dl, que desde cierta distancia parecen cargas puntuales, determinamos el campo en una superficie normal a la línea de carga, aplicando superposición.

No debemos olvidar que E es un vector, con dirección r, por lo que si deseamos resultados escalares debemos integrar sus componentes, según una línea paralela a la línea de carga y otra paralela a la normal, la integral se debe extender entre los límites -¥ a +¥ .

El resultado de la integral que se busca entre los valores de l, límites -¥ e ¥ :

El campo que se determina es bidimensional, no se distingue entre una superficie normal al conductor y otra.

Vale comparar el campo bidimensional debido al conductor indefinido (punto o círculo en el plano), con el campo tridimensional debido a una carga puntual, (esférica en el espacio), el campo tridimensional varía con la inversa de r², y el campo bidimensional en cambio varía con la inversa de r.

El potencial debido a un conductor rectilíneo indefinido se determina integrando el campo eléctrico:

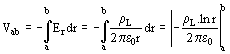
Se observa la diferencia con el potencial debido a una carga puntual en el espacio (tridimensional) que es proporcional a 1/r, el potencial en el infinito (para el problema bidimensional) no puede ser determinado, mientras que lo pudimos adoptar nulo para el problema de la esfera cargada (tridimensional).

Con estas fórmulas se puede determinar el campo alrededor de un conductor, de un haz de conductores.

El cilindro, o el haz de cilindros se utilizan para hacer una representación de una línea con sus conductores únicos o en haz, a los que se aplican distintos valores de tensión en cada instante obteniéndose el campo eléctrico en la superficie de los conductores.

También es de interés determinar el campo eléctrico en el suelo debajo de la línea eléctrica, o en general en un punto cualquiera del espacio.

La relación tensión y cargas en los conductores de una línea multifilar es:

La matriz C cuadrada incluye coeficientes de capacidad (que no deben confundirse con las capacitancias de los conductores), se obtiene invirtiendo la matriz l , de coeficientes de potencial, que se construye de la siguiente manera.

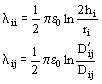
siendo:

Si los conductores son en haz se los puede representar todos uno por uno, y luego reducir la matriz de coeficientes, o bien el valor de ri debe representar un conductor con el radio equivalente del haz. Para esto si es dato DM distancia entre los n conductores, el radio del haz es R.

El radio equivalente resulta:

donde:

Este corresponde a un conductor único ficticio que presenta la misma capacitancia que el haz con todos los conductores vecinos.

Ya se determinaron las matrices [l ] y [C], la relación para calcular las cargas en los conductores de una línea multifilar es:

Se determina la carga eléctrica en los conductores y el gradiente medio, considerando las tensiones aplicadas en un instante a cada conductor.

Se admite que el campo alrededor del conductor varía conforme a la siguiente expresión, obteniéndose de ella los máximos y mínimos.

donde J es el ángulo de la dirección del campo respecto de la dirección radial.

Se observa un factor de aumento del campo que tiene un máximo, y un mínimo a medida que se rodea el conductor. Finalmente se tienen datos para ver el máximo campo que se presenta, lo que permite la evaluación de otros efectos de interés.

El efecto corona designa el conjunto de fenómenos ligados a la aparición de conductividad de un gas (aire) en la proximidad de un conductor sometido a alta tensión.

La conductividad es debida a un fenómeno de ionización, en el aire existen pares iones(+) electrones libres(-), creados por la radiación cósmica o radioactividad natural. Estos sometidos a un campo eléctrico muy intenso son acelerados y chocan generando más iones.

El conductor, cuando está sometido a un fuerte efecto corona, presenta una luminosidad en la obscuridad, y una crepitación ininterrumpida, presentándose pérdidas en el tubo corona, que se deben principalmente al movimiento de los iones.

La tensión a la que aparece este fenómeno se denomina, tensión crítica de corona, o tensión de inicio de corona, que es función de la tensión, del diámetro de los conductores, de la distancia entre ellos y de las condiciones atmosféricas.

Con el aire seco este efecto resulta prácticamente insignificante pero al variar las condiciones climáticas, las pérdidas correspondientes pueden llegar a alcanzar valores económicamente considerables.

Para dos conductores paralelos que tienen el mismo potencial, cuyo diámetro es d, distanciados en a, en la zona donde se tiene la menor línea de campo, cuando la relación a/d > > 1 se calcula la intensidad de campo periférico, con la expresión:

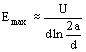
Para las líneas de altísima tensión, la solución racional consiste en la utilización de haces de conductores como se indica en la figura 4.4, el efecto es como si se tuviera un conductor único con un diámetro equivalente elevado, del orden del diámetro del haz.

Peek propuso una fórmula que permite determinar el campo crítico de un conductor cilíndrico:

donde:

El estado de la superficie del conductor es muy importante, la relación precedente vale para superficies pulidas, a medida que la superficie no es pulida el campo critico se reduce, para tener en cuenta este efecto se utiliza un factor m < 1.

Para el conductor de alambres el campo superficial varía sensiblemente, las imperfecciones de la superficie son un factor determinante en la práctica.

También las condiciones atmosféricas juegan un rol importante, lluvia, neblina, rocío, son causa de gotas de agua en la superficie del conductor, reduciendo el valor del campo crítico.

El factor m tiene un valor 0.9 para un estado normal de la superficie, la lluvia puede reducirlo hasta 0.6 y en algunos casos aun menos.

Asociados al campo eléctrico superficial se presentan fenómenos de radiointerferencia (causados por el campo), perturbaciones que afectan a la radiorecepción.

Este efecto es particularmente molesto en las zonas pobladas que son atravesadas por líneas, o en la proximidad de estaciones eléctricas.

Estando sometidos los conductores a cierta tensión se detecta el nivel de perturbación mediante un receptor definido, para completar la medida se debe determinar:

En la instalación en servicio parte de la radiointerferencia es generada por las piezas metálicas (que se encuentran bajo tensión), y parte por las aislaciones contaminadas, cuya influencia crece con la presencia de humedad.

También se presentan perturbaciones en frecuencias de televisión y radiofrecuencia en frecuencia modulada.

Otra perturbación que aparece es el ruido acústico, que también se incrementa con el mal tiempo.

Buscando la solución de estos problemas, debemos orientarnos a la reducción del campo eléctrico en la superficie del conductor, esto hoy se consigue con haces de conductores, y es así que en 220 kV abundan las líneas con haz de 2 conductores, también a veces hasta 500 kV, en 400 y 500 kV hay líneas con 3 conductores, y en 500 y 800 kV con 4 conductores.

Cuando se observan soluciones del pasado se encuentran líneas de solo un conductor de diámetro importante, construido especialmente para limitar el efecto corona, se trata de un conductor que llama poderosamente la atención por ser hueco, obsérvese la figura 4.5 que nuestra el conductor hecho con planchuelas conformadas, y la figura 4.6 con un conductor de haz de alambres cableado sobre un alambre en espiral para lograr un alma hueca, soluciones estas que no han soportado la comparación económica con haces de cables convencionales, y ya no se conciben como solución posible.

Observamos también que son muy comunes los cables de aluminio con alma de acero, esto no es para aumentar el diámetro sino por la resistencia mecánica. Mientras observamos soluciones de cables especiales, llamamos la atención sobre un cable de alta resistencia, en el cual la sección de acero supera ampliamente la sección del material conductor (aluminio), se trata de un cable que cubre un vano muy grande (3.5 km aproximadamente, el cruce del estrecho de Messina entre Italia y la isla de Sicilia), ver figura 4.7.

La seguridad en la transmisión de potencia exige una gran aislación de la línea. Una regla práctica exige una tensión de arco en seco (no bajo lluvia) de tres a cinco veces el valor de tensión nominal de la instalación. La tensión de descarga externa de una cadena de aisladores es con buena aproximación proporcional a la distancia a tierra.

Los aisladores se comportan como si el espacio que ocupan se reemplazara por aire, quedan entonces los electrodos metálicos que corresponden a soportes vinculados a tierra y conductores en tensión.

Cada uno de los aisladores de la cadena tiene una capacidad propia entre las partes metálicas que constituyen su unión (K), una capacidad con relación al poste (C) y una capacidad con relación al conductor (C*), pudiéndose considerar este conjunto como una cadena de capacidades, como se indica en la figura 4.8.

Cálculos y mediciones muestran que la distribución de la tensión a lo largo de la cadena de aisladores no es uniforme, es decir, los diversos elementos no representan 1/n de la tensión total, en el caso que la cadena esté constituida por n elementos.

Este tipo de configuración aparece frecuentemente en la electrotecnia de tensiones elevadas, por ejemplo, para los devanados de los transformadores y de las máquinas, con efectos especialmente importantes en el caso de tensiones de impulso.