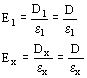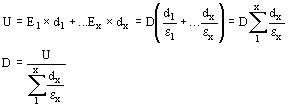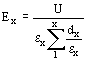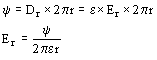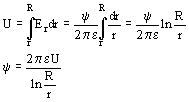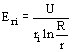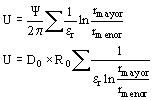APENDICE
Problemas de aplicacion
A continuación se desarrollan y enuncian algunos problemas, que están relacionados con los capítulos de la materia.
Estos problemas reflejan algunos aspectos que se pueden presentar en el ejercicio de la profesión, y que resultan de utilidad para que los alumnos aplicando los conceptos teóricos que han adquirido en ésta y otras asignaturas, experimenten y logren una mejor comprensión de los mismos.
Los alumnos deben tratar de resolver estos problemas ansiosos de aprender, tendrán dificultades, y en las sucesivas materias de aplicación, con una visión más amplia de los distintos argumentos, lograrán obtener distintos enfoques.
Esperamos con esto ayudar en su formación, y solicitamos a los alumnos su colaboración para seguir mejorando nuestra función.
1-2. Instalaciones de corriente alterna de alta tensión, instalaciones de alta tensión en corriente continua.
Problema 2.1
A lo largo de un camino corre una línea de 13.2 kV, de 20 km de longitud, al final de la cual hay un pueblo alimentado con varios transformadores sumando 1 MW la carga, usaremos la planilla (ver nota), y aceptamos la hipótesis que las restantes variables del problema son independientes de la tensión (reactancia, resistividad, capacitancia)
Obtenemos características que quedan definidas para la línea, sección 44 mm2, perdidas 7%, Qx y Qc despreciables respecto de la carga...
Obsérvese que la sección no es un valor normalizado, cámbielo adecuadamente, el material puede ser identificado por su resistividad, ¿qué material propone la planilla?
Nota:
Para ayudar a resolver rápidamente, en modo aproximado, este problema y los siguientes, se ha preparado una planilla que contiene las fórmulas, y permite obtener las soluciones numéricas (
bajar planilla Atpr2-1.zip, luego expandirla y levantarla con Excel)
Problema 2.2
Nuestro ojo no esta perfeccionado para garantizarnos que la línea es de 13.2 kV, nos asalta la duda de que fuera de 33 kV, manteniendo los demás datos, ¿cuáles serían los resultados?
La sección necesaria se reduce a 17 mm2, con esta sección el conductor es muy débil, las secciones mínimas que se utilizan en las soluciones constructivas son mayores.
Varíe la sección a valores normales, cambie de material, busque ventajas e inconvenientes, una ventaja es el precio del material conductor.
Problema 2.3
Suponiendo la línea de 33 kV se piensa poner en el pueblo una industria que consumiría 3 MW más, dando un total de 4 MW, ¿cuál sería la línea?
La sección necesaria es ahora 69 mm2, y las pérdidas 3%, comparando con los resultados del problema 2.1 se observa la conveniencia del desarrollar obras con tensión más elevada, tienen más capacidad para el futuro, mejor rendimiento... pero tienen más costo.
Problema 2.4
Observamos una línea de 132 kV, de 100 km que llega a una ciudad cuya carga es 40 MW.
Los resultados que observamos son, sección 175 mm2, pérdidas 4%, Qx = 3 MVAr, Qc = 6 MVAr
La capacidad de una línea de esta tensión es indudablemente mayor, si pensamos en transmitir 100 MW que pasa?
Las secciones normalizadas son otros valores, propóngalas, observe como cambian los resultados.
Problema 2.5
Entre
Futaleufú y Madryn hay dos líneas de 330 kV de 550 km que transmiten 350 mW, veamos que resultados nos muestra la planilla.
Cargando una sola línea con estos datos tenemos sección 612 mm2, pérdidas 8%, Qx = 185 MVAr, Qc = 188 Mvar
Si en cambio ponemos ambas líneas en servicio (cada una esta cargada con la mitad) resulta: sección 306 mm2, pérdidas 8%, Qx = 46 MVAr, Qc = 188 MVar, recordemos que ahora están en servicio ambas líneas por lo que en rigor sección y Q se duplican, las pérdidas en cambio se dan en valor relativo, y su valor se mantiene.
Los datos reales de estas líneas están contenidos en documentos a disposición del público llamados guías de referencia, y que pueden consultarse, la línea que estamos examinando esta formada por dos conductores por fase según norma Canadiense y que se identifican bajo el nombre de EGRET.
¿Cuál es la sección real de esta línea? Para ajustar entonces el problema se debe hacer una comparativa ajustando la densidad de corriente, anímese y haga el cálculo, compare las dos condiciones de servicio con sólo una terna (contingencia) y con ambas ternas (situación normal).
Problema 2.6
La obra que comentamos antes pudo también hacerse en otras tensiones, pruebe con 220 kV y con 500 kV e intente sacar alguna conclusión.
Observe la sección que el programa le propone para la línea de 500 kV, busque soluciones reales y compare la sección del conductor. Varíe la densidad de corriente para que la sección corresponda a 4 conductores DOVE.
Problema 2.7
Cada tramo del
sistema Chocón Buenos Aires (Alicura Abasto) es de 350 km y transmite 1000 MW, veamos que resultados obtenemos:
sección 1154 mm2, pérdidas 3.6%, Qx = 420 MVAr, Qc = 270 Mvar...
Cada línea está formada por un haz de 4 conductores, las nuevas por otro conductor PEACE RIVER de tamaño parecido, la transmisión total es de 3 tramos... las pérdidas son entonces 3 ´
3.6%, las potencias Qx y Qc involucradas son considerando 12 tramos...
El
esquema geográfico de la Red Eléctrica de la República Argentina puede obtenerse buscando en la dirección siguiente: http://www.cammesa.com.ar/ donde se presenta abundante información de la red eléctrica argentina (además del esquema geográfico, el diagrama unifilar, para llegar a este: buscar MEMNet, Publicaciones MEMNet, Informes varios, Esquemas de la red eléctrica).
Problema 2.8
Con los datos del problema 2.5 propóngase una transmisión en corriente continua, utilice distintas alternativas de tensión y número de polos.
Problema 2.9
La distancia Chocón Buenos Aires supongámosla de 3 ´
350 km, imagínese una transmisión en continua de 1000 km expreso (sin estaciones intermedias) de 1000 MW, y de 2000 MW... ¿qué puede proponer?
Problema 2.10
Difícilmente uno trabaja en grandes sistemas de transmisión, pero todos en la profesión tienen que ver con plantas industriales de potencias y tamaños limitados.
Volvamos a un problema de media tensión, se debe alimentar una carga de 3 MW, si se la alimenta en 13.2 kV y se desean limitar las pérdidas al 5% a que distancia puede estar ubicado el centro de alimentación? Y si fuera en 33 kV?
Como aclaración a estos problemas es importante destacar que la realidad no es tan fácil, hay muchas otras consideraciones que se deben hacer antes de decidir orientarse a una solución.
Los problemas que hemos planteado requieren también desarrollar muchas otras evaluaciones, la obra debe funcionar durante muchos años económicamente, debe adaptarse a un futuro incierto, debe dar el servicio en condiciones técnicas (llamadas hoy calidad de servicio), debe afectar el ambiente lo menos posible (hoy llamado impacto ambiental).
Esto sólo pretende dar el primer paso, ayudar a orientar algunas características de las líneas de alta tensión que son una parte enorme de la inversión del sistema eléctrico.
3. Procesos electromagnéticos oscilatorios y de choque.
Problema 3.1
Para una red de 500 kV (máxima de servicio 525 kV) basándose en estudios estadísticos de sobretensiones de maniobra (SIL), que se realizan utilizando programas de computadora que resuelven las ecuaciones diferenciales que corresponden al sistema eléctrico (ATP), se tiene que la máxima sobretensión alcanzada es del orden de 1.8 a 1.85 pu.
Cuando se utilizan como elementos de protección descargadores de óxido de zinc, el SIL del equipamiento debe ser igual o mayor de 1.4 pu de la máxima sobretensión de maniobra.
Se desea saber como se deben especificar los niveles de aislación de un transformador de potencia que debe ser instalado en dicha red.
El valor de pico de la tensión de fase es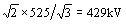 , por lo tanto cuando se tiene una sobretensión de 1.85 pu el valor de la tensión de fase resulta 1.85 ´
429 = 793 kV.
, por lo tanto cuando se tiene una sobretensión de 1.85 pu el valor de la tensión de fase resulta 1.85 ´
429 = 793 kV.
Con descargadores de óxido de zinc, el equipamiento debe poder soportar como mínimo una sobretensión de impulso de maniobra de 1.4 ´
793 = 1110 kV.
La norma de transformadores de potencia IEC 76-3 "Insulation levels and dielectric tests" en la Tabla V, para la tensión Um = 525 kV fija los siguientes valores de tensión de impulso de maniobra: 1050 y 1175 kV. Como el valor calculado es 1110 kV corresponde adoptar el valor de tensión de ensayo de 1175 kV.
Además la Tabla en correspondencia con la tensión de ensayo a impulso de maniobra indicada, fija dos valores de tensión de ensayo a impulso atmosférico (BIL), 1425 y 1550 kV.
Queda a criterio de quien debe especificar los niveles de aislación, adoptar para esta tensión de ensayo, el valor más representativo de las reales condiciones de solicitación a impulso atmosférico a las que estará expuesto el transformador en servicio.
4. El campo eléctrico
Problema 4.1
Determinar el campo eléctrico en la superficie de los conductores en haz de una línea de 500 kV (medio de un vano) cuyos datos y distancias se indican en las figuras.
La
figura a4.1-1 corresponde al centro del vano, la figura a4.1-2 al punto donde el conductor está sostenido en la torre, los dos resultados dan el rango dentro del cual los valores varían en el vano.
Hacer una tabla resumen y comparar los resultados para conductor central, lateral en el centro del vano y en el extremo.
Comparar con los valores que se obtienen sin los cables de guardia.
Una de las posibilidades de resolver este problema es utilizando el programa CORCAM cuyas características principales se describen a continuación.
El programa calcula el campo eléctrico sobre conductores con el método propuesto por CIGRE, (Perturbations engendres par l'effet de couronne des reseaux de transport 1974), considerando la influencia de la tierra y los cables de guarda, y realiza el cálculo de los parámetros de la línea representada.
Para la resolución de este problema los cables de guarda se consideran a tierra, asumen cierta carga y tienen influencia sobre el campo superficial del conductor de fase, (cuando están aislados asumen una tensión y su carga es nula).
Los datos se deben preparar de acuerdo a lo que indica CORCAM.TXT, se han preparado dos lotes de datos TAT001.DAT y TAT002.DAT.
Se ingresan para cada haz de conductores los datos que lo describen:
Para cada uno de los cables de guarda se ingresan los datos con los valores organizados de la misma manera que para los conductores.
A continuación se ingresan pares de valores para cada conductor que corresponden a tensión y ángulo.
El último registro indica el ángulo de incremento en grados, para analizar el fenómeno en el transcurso del tiempo.
El valor del campo máximo es 16.865 kV/cm para el centro del vano, y las capacitancias (simetrizadas) de secuencia directa 13.34 picoF/km, y de secuencia cero 11.189 picoF/km.
Para la suspensión en cambio los resultados son 16.454 kV/cm, capacitancias 12.653 y 8.757 picoF/km.
Problema 4.2
Para líneas de alta tensión se deben realizar ensayos para verificar la presencia de efecto corona visible en las cadenas de aisladores y su correspondiente morsetería. También es importante determinar si los niveles de radio interferencia (RIV) no superan los límites fijados.
Estos ensayos pueden realizarse en instalaciones al aire libre o bien en una sala de ensayos que tiene paredes y techo metálicos.
- En una instalación de ensayos al aire libre se desea probar el haz de conductores de la línea de 500 kV arriba especificado, la distancia al suelo es de 5 m, el haz es único, no están las fases laterales.
- En rigor hay un edificio metálico lateralmente al área de prueba, la distancia al edificio es de 4 m, y el edificio es de gran altura, ¿cómo es el campo considerando la presencia del edificio?
Utilizar el método de las imágenes, hacer la imagen del conductor debida al edificio la tensión aplicada al conductor imagen desfasada 180 grados, ¿por qué?
Lotes de datos TAT011.DAT y TAT012.DAT, y con ellos se han obtenido los resultados siguientes:
- campo superficial 17.313 kV/cm.
- campo superficial 19.671 kV/cm.
Estos valores deben compararse con los que corresponden a la línea del problema anterior, se nota que para lograr que las exigencias del ensayo igualen a las de la línea, es necesario ajustar la tensión aplicada en el ensayo.
Problema 4.3
Los ensayos se hacen en una sala de 15 m entre paredes, 20 m de altura, el cable está suspendido a 5 m del suelo y 4 m de una pared lateral (a 11 m de la otra).
Aplicando el método de las imágenes, se rodea el conductor con sus primeras imágenes, en rigor deberían considerarse infinitas imágenes, experimentar con más capas de imágenes, extraer conclusiones.
Lotes de datos TAT013.DAT y TAT014.DAT, y con ellos se han obtenido los resultados siguientes:
- con 14 imágenes 20.015 kV/cm.
- con 24 imágenes 19.822 kV/cm.
Problema 4.4
Campo eléctrico alrededor de conductores y cadenas de aisladores
Se trata de estudiar el campo eléctrico que se presenta alrededor del conductor de una línea, y de las cadenas de aisladores que soportan el conductor (para estudiar la solución
hacer click).
Problema 4.5
Plantear y resolver el problema de la distribución de la tensión a lo largo de una cadena de aisladores considerando las distintas capacitancias, de aisladores, aisladores a tierra y aisladores a conductor. Observar la no uniformidad de la distribución (para estudiar la solución
hacer click).
5. Aislantes sólidos en la técnica de la alta tensión.
Problema 5.1
El conductor de un devanado de un alternador alojado en una ranura según muestra la
figura a5.1-1 , está aislado contra masa con micanita cuya constante dieléctrica es e
r = 5 y su espesor es l1 = 4 mm.
Entre la pared de la ranura y el aislante del conductor se tiene un delgado estrato de aire (e
r = 1) cuyo espesor es l2 = 0.2 mm.
Si la tensión contra masa es igual a 7.62 kV se requiere calcular el gradiente en el aire, y hacer un breve comentario acerca de su valor.
Sobre la micanita se aplica normalmente una capa de pintura semiconductora (que se comporta como conductora), explicar cual es su efecto y que ventajas se obtienen.
Problema 5.2
Se propone estudiar el campo eléctrico para algunas configuraciones interesantes que se presentan en las máquinas y equipos eléctricos de alta tensión.
Dada la dificultad que implica encarar la resolución de estos problemas con métodos analíticos, se utiliza un programa de cálculo que resuelve el problema mediante un método numérico.
Los datos se esquematizan sobre una retícula regular donde se fuerza la configuración simplificada del objeto alrededor del cual se desea estudiar el campo.
El resultado deseado se obtiene en un archivo de salida que se visualiza con un programa auxiliar.
A modo de ejemplo se plantean los siguientes casos particulares:
- El terminal de un cable de alta tensión es un elemento muy delicado de la instalación, se desea estudiar el campo cuando el terminal se realiza simplemente cortando la aislación (sin ningún tipo de terminal de control de campo). En media tensión sobre la aislación se tiene una pantalla conductora, obsérvese el campo donde esta termina.
Explicación del caso 1 (método de análisis de los resultados obtenidos).
El programa POTRES resuelve la ecuación diferencial de Laplace, en los casos plano (bidimensional x, y) y de simetría alrededor de un eje (también bidimensional, r, z).
Se plantea estudiar la distribución de potencial en el aislante de un cable, y se esquematiza el problema dentro de un área cuadrada, (ver archivo potres1.dat) un lado representa el conductor a potencial 100% (Q), un segmento representa la pantalla a potencial 0 sobre la superficie del aislante, el espacio esta relleno de aislante (representado por X, e
= 5) y aire (I, e
= 1), la separación entre aislante y aire está representada por L.
El límite del espacio (cuadrado) debe estar formado por líneas equipotenciales o líneas de campo (y no se dispone en este programa de otra posibilidad).
El problema se ha planteado preparando los datos, y el ejemplo se ha resuelto como plano observándose el resultado obtenido en la
figura a5.2-1, esto es lo que puede obtenerse de un programa que sólo considere casos planos, si en cambio se resuelve el problema como simetría cilíndrica, suponiendo el conductor con radio 3 (unidades de cuadricula) se obtiene un gráfico figura a5.2-2 con cierta diferencia, que particularmente se aprecia en la proximidad del conductor (eje), si el radio se incrementa, a medida que se hace muy grande se reproduce nuevamente la figura a5.2-1 (que puede considerarse corresponde a radio infinito).
En esta esquematización se ha fijado con potencial cero el lado opuesto al conductor, en alguna medida puede considerarse que representa un caño metálico a tierra que contiene el cable.
Si se considera que el cable esta en el aire, y no dentro de un caño, se puede plantear entonces que el espacio analizado está completamente rodeado de líneas de campo, la verdad quizás sea un caso intermedio...
Resolvamos el problema en estas condiciones, el resultado del cálculo mostrado en la
figura a5.2-3, intuitivamente no se entiende muy bien, si repetimos el cálculo reduciendo el error (diferencia máxima ente sucesivas iteraciones) obtenemos una figura a5.2-4 que es ligeramente distinta.
El hecho de que al variar el error se obtenga una figura distinta pone en evidencia que el programa no obtiene un resultado correcto.
Existe otra posibilidad de variar los resultados, el programa cuando inicia asigna un potencial medio a todos los puntos en los cuales se debe calcular el potencial, esto se ha hecho para ayudar al programa a llegar más rápido a la solución correcta, este valor es propuesto por el programa pero puede asignarse al inicio en forma arbitraria, el valor que el programa asigna en el caso de la
figura a5.2-3 es aproximadamente 80%, si asignamos ahora 20% a este valor obtenemos la figura a5.2-4 que parece mas acertada.
Se trata entonces de probar con otros valores hasta haberse convencido que los resultados no dependen del límite de error, ni del valor inicial... mientras se nota esta dependencia seguramente los resultados obtenidos no son todavía correctos, pese a que el criterio de fin del cálculo está satisfecho.
Es importante realizar un cuidadoso análisis crítico de los resultados obtenidos y convencerse que se satisfacen las leyes de la física, antes de extraer conclusiones, que podrían basarse en algo erróneo...
Sobre la aislación se dispone un par de conos cuya función es controlar el campo eléctrico, compárese los resultados de este caso con el anterior.
Sobre el cono de expansión que está del lado del cable se dispone una capa conductora, el cono de expansión del lado extremo se deja sin cubrir, compárese este caso con los anteriores, obsérvese la ventaja de utilizar el cono de expansión.
Se trata de un aislador pasamuros para interior que tiene una superficie lisa y forma de tronco de cono. Obsérvese el campo eléctrico en su interior y en el aire. Analícese como influye un aumento de longitud del cono en los valores máximos del campo eléctrico en el material del aislador.
Un aislador pasamuros para exterior se caracteriza por tener polleras o campanas cuya función es lograr en poca distancia una línea de fuga importante para controlar el efecto de la contaminación. Obsérvese el campo eléctrico para este diseño y compárese con el caso anterior.
Los aisladores soporte cumplen la función de mantener separados de tierra las partes en tensión, es importante estudiar la configuración del campo eléctrico tanto dentro del aislador como en el aire que lo rodea. En particular muchos aparatos eléctricos (seccionadores, interruptores) tienen aisladores de este tipo, de aquí la importancia de estos estudios.
En los casos de tensiones elevadas para uniformar el campo se dispone de un anillo de guarda en su parte sometida a tensión, compárese con el caso anterior observando las diferencias de campo que se presentan. Este artificio se utiliza también para controlar la uniformidad del campo eléctrico dentro de los descargadores de sobretensión.
Resulta interesante estudiar el campo cuando se tiene una disposición varilla - plano, es decir una punta que se encuentra a un potencial dado y un plano que está a potencial de tierra.
Analice el campo de un aislador de suspensión de una línea aérea, a partir de una figura del mismo, realice la esquematización en un retículo suficientemente denso, prepárese el lote de datos, y obsérvense los resultados.
Configuración del campo eléctrico que se tiene en el extremo de un devanado de un transformador de alta tensión, teniendo en cuenta la presencia de los elementos de fijación (prensayugos) y soporte de las bobinas que se encuentran a potencial de tierra.
Los extremos de bobinas de un alternador sincrónico se encuentran a un determinado potencial, el paquete magnético a potencial de tierra, estudiar la configuración del campo en esta parte y hacer las observaciones que correspondan.
Problema 5.3
Los cables aislados, de baja y de alta tensión se fabrican en forma continua y se enrollan en bobinas de longitudes adecuadas a una conveniente manipulación. Uno de los ensayos que demuestran la calidad consiste en aplicar a la aislación cierta tensión durante cierto tiempo, y comprobar que no se presentan descargas.
Es necesario que la aislación quede sometida a la tensión de prueba, esto no es difícil para los cables que tienen sobre la aislación una lámina conductora (pantalla) pero en el caso de los cables que no tienen se los prueba sumergiendo la bobina en un tanque de agua, los extremos del cable se mantienen fuera del agua y se aplica cierta tensión de ensayo entre conductor y tanque (agua).
Examinamos un caso en el que se aplica tensión mediante un transformador que tiene una tensión en vacío de 4000 V y una corriente de cortocircuito de 1 A.
Se ensayan cables de aproximadamente 0,33 microF/km, y se observan algunos fenómenos que son interpretados como anómalos por quien está realizando estas pruebas.
El operador del ensayo observa que con distintas bobinas (de distinta longitud) se presentan corrientes de ensayo que no son proporcionales, como él cree debería ser.
Por otra parte parece que las tensiones aplicadas a las bobinas son distintas de los 4000 V que el operador cree aplicar.
Se pide a la oficina técnica que explique las observaciones y determine que significan los ensayos de las muestras.
El problema esta resuelto en una planilla de cálculo (ver nota), en la que se pueden cambiar los datos, para lograr determinar las distintas condiciones de ensayo.
Se determina la fuente de Thevenin equivalente, en particular su impedancia (reactancia), se determina por otra parte la impedancia por unidad de longitud del cable, y para distintas longitudes de bobinas sus reactancias capacitivas.
Con la impedancia total del circuito, para cada longitud surge la corriente absorbida y la tensión aplicada al capacitor equivalente al cable, el gráfico que relaciona longitud y tensión sobre el cable muestra cierta curvatura, que pone en evidencia la no linealidad de la relación entre longitudes y tensiones de ensayo, y explica brevemente las perplejidades del operador antes comentadas.
Nota:
Para este problema se ha preparado una planilla que permite obtener los valores de interés (
bajar planilla Atpr5-3.zip, luego expandirla y levantarla con Excel)
Problema 5.4
Las configuraciones geométricas más frecuentes en los equipos eléctricos son la de un capacitor de placas paralelas, campo homogéneo, pues todos los puntos del dieléctrico se encuentran a idéntica solicitación (estrictamente si las placas tienen superficie infinita), otra es la cilíndrica coaxial, es decir el conductor interno energizado y el externo a tierra, siendo en este caso la solicitación interna no homogénea.
Un material cuya rigidez dieléctrica E = 60 kV/cm se lo somete a las siguientes pruebas: entres dos placas separadas 1.5 cm y entre dos cilindros coaxiales cuyos diámetros son 2 y 5 cm respectivamente, calcular el potencial de ruptura en cada caso.
a) Campo homogéneo 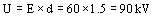
b) Campo no homogéneo 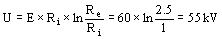
se observa que si bien el espesor del dieléctrico es el mismo en ambos casos, sin embargo en la solicitación del campo no homogéneo, el material soporta sólo el 61% del caso de campo homogéneo tomado como referencia.
Problema 5.5
El campo eléctrico que llega a una frontera entre dos medios dieléctricos experimenta una refracción (cambio de dirección).
Si el campo es perpendicular a la frontera se tiene que 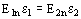 , si en cambio es tangencial a la frontera resulta
, si en cambio es tangencial a la frontera resulta 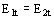 .
.
Cuando el campo llega a una superficie con una dirección cualquiera, se puede descomponer en dos componentes una perpendicular y otra tangencial a la frontera.
Explicar que ocurre con cada uno de las componentes del campo que llega a una superficie de un aislador con una dirección cualquiera, por ejemplo una frontera porcelana - aire (siendo e
r de la porcelana de 6 a 7 veces mayor que el del aire).
Problema 5.6
Capacitor plano con armaduras paralelas
En un capacitor plano con armaduras paralelas (campo uniforme) con varias capas de distintos dieléctricos en serie al cual se le aplica una tensión alterna U, las distintas capas son solicitadas por gradientes inversamente proporcionales a las respectivas constantes dieléctricas.
Todos los estratos serán atravesados por un flujo dieléctrico común y
= A´
Dx, siendo A la superficie de la armadura.
La inducción dieléctrica será por lo tanto la misma en cada uno de los estratos
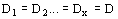
por lo tanto el gradiente en cada capa resulta
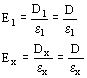
La tensión aplicada resulta
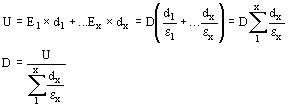
por lo tanto el gradiente para una capa dada resulta
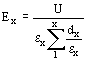
Siendo el valor de la sumatoria el mismo para todos los aislantes en serie, el más solicitado de los aislantes es que tiene la constante dieléctrica más pequeña.
Se puede afirmar que la disposición óptima de los aislantes en serie corresponde a aquella que utiliza materiales que tienen en común el producto e
r ´
Er (en la práctica valores no muy distintos).
Esto se verifica particularmente en los transformadores en aceite, cuando entre dos arrollamientos separados por un canal de aceite (e
r = 2.2) se interpone un cilindro de papel impregnado (e
r = 4.2). Suponiendo que los radios de los cilindros son suficientemente grandes como para considerar planas las paredes de los cilindros se puede asimilar a un capacitor plano.
El gradiente en el aceite se incrementa respecto al valor que tenía antes cuando solamente se tenía aceite, y el aumento es tanto más grande cuanto mayor es el espesor del cilindro.
El cilindro de papel resulta igualmente útil debido a que interrumpe la continuidad del aceite que puede contener en suspensión impurezas, que alineándose en el sentido del campo, pueden provocar la descarga.
Es importante optimizar los diseños de los aislamientos de los transformadores incrementando la resistencia dieléctrica con volúmenes no mayores de los requeridos, reduciendo de este modo el tamaño, peso y costo del transformador.
La reducción del volumen aislante requiere un conocimiento completo de la función de los aislantes líquidos y sólidos.
La aislación sólida se utiliza formando barreras para subdividir los canales de aceite altamente solicitados en canales más estrechos. La
figura a5.6-1 muestra un esquema de la parte superior del devanado de alta tensión, la disposición de estas estructuras aislantes debe realizarse siguiendo las líneas equipotenciales para minimizar los esfuerzos tangenciales en el papel.
Siendo el aceite el elemento más solicitado, por su menor permitividad relativa, el espesor del canal se puede estimar según la
figura a5.6-2, que muestra la rigidez dieléctrica en corriente alterna (kVmax/cm) en función del espesor (mm), para aceite en distintas condiciones.
Los campos dieléctricos en las máquinas y aparatos eléctricos no son casi nunca uniformes, como en el caso antes considerado, el cálculo del gradientes es variable de un punto a otro y en muchos casos se lo puede asimilar a un campo cilíndrico.
Capacitor cilíndrico con varias capas dieléctricas
Veamos el caso de un capacitor cilíndrico con varias capas dieléctricas cuyas armaduras tienen respectivamente un radio interno r y externo R, siendo y
el flujo dieléctrico que pasa de una armadura a otra y que es el mismo que atraviesa todos los estrados dieléctricos.
Por unidad de longitud, suficientemente alejado de los bordes se tiene que
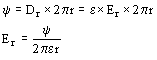
La tensión aplicada resulta
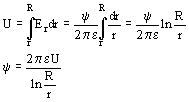
finalmente para un radio ri cualquiera el gradiente resulta
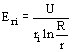
El gradiente en cada punto del campo es por lo tanto inversamente proporcional a la distancia del punto al eje del capacitor y su diagrama es una hipérbola como corresponde al ejemplo de la
figura a5.6-1.
Otro caso que se lo puede estudiar como un capacitor cilíndrico es el aislador pasante de alta tensión de un transformador
figura a5.6-3, donde se puede observar que el electrodo externo es menos largo que el interno, donde para obtener una mejor distribución del gradiente se interponen en la masa aislante delgadas capas metálicas.
En este caso se tiene aproximadamente
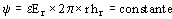
siendo hr la altura de la lámina metálica interpuesta en correspondencia al radio r. Si se quiere que el gradiente Er se mantenga constante, hr debe variar inversamente proporcional al radio r, es decir los bordes de la armadura se deben encontrar sucesivamente sobre los puntos de una hipérbola equilátera.
Método de cálculo de un capacitor plano
Son datos los espesores di, las constantes dieléctricas e
i, la tensión aplicada U
Se determina D = U / sumatoria (di / e
i)
Se miden las distancias desde una de las placas, x y se avanza dx
Se puede representar en función de x
El campo Ex = D / e
x
También se determina Ux = U(x-dx) - Ex ´
dx que se repite a lo largo de x
Método de cálculo capacitor cilíndrico
Lo mismo se hace para el capacitor cilíndrico, para este además se debe conocer el radio interno R0
Se determina Dr = y
/ (2 ´
p
´
r)
Donde r inicia a partir de R0, se considera que
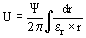
Como la integral es discontinua por los saltos de e
r se deben sumar las integrales entre discontinuidades sucesivas, obteniéndose el valor de D0
D0 = y
/ (2 ´
p
´
R0)
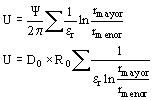
Se miden las distancias desde R0 y se avanza dr
Se puede representar en función de r
El campo Er = Dr / e
r = D0 ´
R0 / (r ´
e
r)
También se determina Ur = U(r-dr) - Er ´
dr que se repite a lo largo de r
Estos métodos se han volcado en una planilla excel (
bajar planilla atpr5-6.zip), que representa las variaciones de E y de U en función de la coordenada geométrica para un capacitor plano, y para uno cilíndrico con capas de distinta constante dieléctrica.
7. Análisis de las exigencias reales a que se hallan sometidos los dieléctricos.
Problema 7.1
Seleccionar descargadores de óxido de cinc para un sistema eléctrico de 69 kV, que esta alimentado por líneas aéreas que llegan desde una fuente relativamente lejana (a los fines de este estudio).
Se han calculado las corrientes de falla a tierra (cortocircuitos monofásicos) en distintas condiciones de la red. Obteniéndose los resultados siguientes:
Caso A – tensiones en las fases sanas mínimo 57.2 kV máximo 65.3 kV
Caso B – tensiones en las fases sanas mínimo 59.42 kV máximo 61.3 kV
Caso C – tensiones en las fases sanas mínimo 58.6 kV máximo 58.8 kV
La corriente total de falla a tierra supera los 1000 A y el sistema esta puesto a tierra a través de reactores zig-zag.
Metodología
En la selección de los descargadores se siguen los pasos indicados en la guía ABB SESWG/A 2300E Technical Information Selection guide for ABB HV surge arresters.
Paso 1 – Obtención de los parámetros del sistema
Obtención de la mayor tensión estimada del sistema Um
(Definición: Tensión máxima del sistema Um es la mayor tensión eficaz fase fase que se presenta bajo condiciones normales de operación en cualquier tiempo y punto del sistema)
Se puede estimar en 1,05 ´
69 kV = 72,45 kV = aprox. 72,5 kV
Condiciones de falla a tierra
En la memoria de calculo de cortocircuito, se han estudiado cortocircuitos monofásicos en distintas condiciones de la red.
Estos valores determinan la tensión TOV Sobretensión temporaria, que ocurre en las fases sanas cuando hay fallas a tierra, en el caso examinado es:
Tensión máxima 65,3 kV.
También puede presentarse durante fenómenos de ferroresonancia, o en rechazos de carga, que son situaciones no previsibles en el sistema en estudio.
El factor de puesta a tierra se determina a partir de este último valor
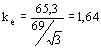
Como este valor supera el límite de 1,4 a los fines de las sobretensiones el sistema que se analiza se considera aislado de tierra
La duración de la sobretensión depende del tiempo de eliminación de la falla que se considera en sistemas puestos a tierra directamente menor de 10 segundos, en sistemas aislados puede superar 2 horas, y entonces la tensión TOV es la compuesta.
En el caso en estudio la corriente total de falla a tierra supera los 1000 A por lo que su duración debe limitarse al valor previsto de los dispositivos de puesta a tierra (en el caso en examen reactores zig-zag) que es de menos de 10 segundos.
Paso 2 – Control de condiciones de servicio anormales
Temperaturas fuera del rango – 40 a + 45 ºC.; frecuencias fuera del rango 15 – 62 Hz; fuentes de calor próximas a los descargadores.
Se considera que no se presentan condiciones de este tipo.
Paso 3 – Control de otras causas de ocurrencia de TOV
Se considera que no se presentan condiciones fuera de las indicadas en paso 1.
Paso 4 – Seleccionar la tensión de operación continua
La tensión de operación continua Uc es la designada como permisible en valor eficaz a frecuencia industrial que puede ser aplicada continuamente (permanentemente) en bornes del descargador.
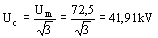
Paso 5 – Seleccionar la capacidad conveniente TOV
La
figura a7.1-1 muestra la capacidad TOV expresada en múltiplos de Ur función de Tr que para 10 segundos es 1,1 con energía previa y 1,14 sin energía previa (este valor depende de marca y modelo de descargador, lo que debe confirmarse una vez adoptado el descargador).
Luego se inicia la selección del descargador:
Selección basándose en la tensión preliminar
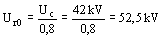
Determinación de TOV basándose en la amplitud y duración de la falla
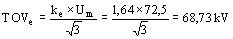
Para sistemas efectivamente aislados se adopta ke = 1,73
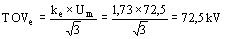
Consideración de energía absorbida previa
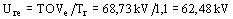
para 10 segundos, con energía previa
Selección del valor final
Se selecciona el mayor valor entre Uro y Ure
Ur £
62,5 kV debiendo adoptarse el valor normalizado 66 kV
Valores adoptados
Aplicación, protección de transformadores y equipamiento en sistemas con sobretensiones atmosféricas y de maniobra.
Los requerimientos de capacidad de energía, contaminación, son moderados
|
Frecuencia |
60 Hz |
|
Tensión del sistema |
72,5 kV |
|
Tensión nominal |
69 kV |
|
Corriente nominal de descarga |
10 kAcresta |
|
Descarga de corriente soportada: |
|
|
alta corriente |
4/10 m
s 100 kAcresta |
|
baja corriente |
2000 m
s 550 Acresta |
|
Capacidad de energía descarga de línea |
2 impulsos 5,1 kJ/kV (Ur) |
|
Prueba de energía nominal |
3,6 kJ/kV (Ur) |
Datos garantizados:
|
Ur kVrms |
66 |
|
Uc kVrms |
53 |
|
MCOV kVrms |
53 |
|
TOV capability 1 sec kVrms |
76 |
|
10 s kVrms |
73 |
|
Ures 30 /60 m
s 500 A kVcresta |
137 |
|
1 kA kVcresta |
142 |
|
8 / 20 m
s 5 kA kVcresta |
165 |
|
10 kA kVcresta |
176 |
|
20 kA kVcresta |
196 |
|
Distancia de fuga (creepage distance) mm |
1660 = 22,9 ´
72,5 > 20 ´
72,5 |
|
(medium pollution) |
|
Aislación externa |
(valores de ensayo con aislador vacío) |
|
LIWL (Lightning Impulse Wave Level)
1,2 / 50 kVcresta |
350 |
|
60 Hz bajo lluvia (10 s) kVrms |
170 |
Los niveles de polución están clasificados en la norma IEC 815, se indican a continuación para cada nivel los valores mínimos de distancia de fuga:
|
Nivel de polución |
Distancia de fuga
(mm/kV Um) |
|
Ligera (L) |
16 |
|
Mediana (M) |
20 |
|
Alta (H) |
25 |
|
Muy alta (V) |
31 |
Problema 7.2
Propagación de sobretensiones debidas a descargas atmosféricas en líneas eléctricas.
8. Especificaciones de ensayos en alta tensión.
Problema 8.1
Para un sistema de 500 kV se desean establecer las distancias de aislación que deben ser utilizados en el diseño de una instalación.
Las tensiones de ensayo para la coordinación de la aislación de acuerdo con la IEC 60071-1 Insulation co-ordination Part 1: Definitions, principles and rules se pueden obtener con M-ENSAYO (ejecutable dentro de WPROCALC), debiéndose elegir aquellos valores que son representativos de las reales solicitaciones del sistema que se analiza, a modo de ejemplo la tabla muestra algunos de los posibles valores:
|
tensión ensayo industrial |
680 kVrms |
|
tensión ensayo de maniobra |
1175 kVcresta |
|
tensión ensayo atmosférico |
1550 kVcresta |
|
tensión ensayo fase - fase |
1800 kVcresta |
La distancia que soporta la tensión de 680 kVrms se obtiene fijando el gradiente de 300 kV/m, lo que da 2,267 m.
Las distancias de maniobra y atmosféricas se determinan con funciones que dependen de la forma de los electrodos, estas distancias se deben determinar para una probabilidad de soportar el ensayo de 90% (10% probabilidad de descarga). Este cálculo es desarrollado por el programa M-FORMA (ejecutable dentro de WPROCALC), la gráfica de los resultados se puede ver en la
figura a8.1-1.
Se observa que si no hubiera solicitación atmosférica, es decir sólo de maniobra, para factor de forma entre 1.6 y 2 el dimensionamiento está impuesto por la solicitación a frecuencia industrial, por debajo de 1.6 por la solicitación de maniobra.
Si además hay solicitación atmosférica entonces entre 1.4 y 2 se dimensiona por solicitación atmosférica, debajo de 1.4 en cambio por solicitación de maniobra.
Valores bajos del coeficiente k obligan a aumentar las distancias, en consecuencia se destaca que debe hacerse cierto esfuerzo para mejorar las formas, y evitar diseños que impliquen factores menores de 1.3 - 1.4.
Las formas de los electrodos se definen con factores que se llaman de espacio (gap factor) propuestos en un estudio de CIGRE, y que pueden verse en el Capítulo 8. "Distancias eléctricas" figuras de los puntos 8.3 y 8.4, del "CURSO DE DISEÑO DE ESTACIONES ELECTRICAS" que se encuentra entre los LIBROS INTERACTIVOS a los que se accede desde la página:
http://www.ing.unlp.edu.ar/sispot.
Problema 8.2
Los diversos ambientes contaminantes se clasifican de acuerdo con los siguientes parámetros:
- Depósito de contaminación salina equivalente a un depósito de cloruro de sodio (mgr/cm2) en función del tipo de aislador soporte o suspensión.
- Distancia de la costa oceánica (km) en función de que la velocidad del viento sea > 10 m/s o < de 10 m/s.
- Cercanía de áreas industriales (lejos, cerca, dentro, contacto directo con niebla marina).
en función de los cuales las normas establecen distintos niveles de contaminación (libre de contaminación, insignificante, leve, moderado, considerable y especial), fijando para cada una de ellas una distancia de fuga mínima recomendada en (cm/kV).
Para un grado de contaminación moderado para el cual la distancia de fuga recomendada es de 3 (cm/kV), se desea determinar la longitud de fuga mínima requerida por una aislador soporte de porcelana cuya tensión de trabajo es 13800 V con un factor de sobretensión de 1,3.
Problema 8.3
La presión y la temperatura de un gas son factores determinantes de su comportamiento dieléctrico. Con la presión se incrementa la densidad, con la temperatura disminuye.
La siguiente relación permite calcular la densidad en función de la presión y la temperatura:
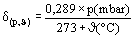
Siendo la rigidez dieléctrica para el SF6 = 89 kV/cm en condiciones normales (20 ºC y 1013 mbar), determinar su rigidez a 40 ºC y 3 bar.
![]() , por lo tanto cuando se tiene una sobretensión de 1.85 pu el valor de la tensión de fase resulta 1.85 ´
429 = 793 kV.
, por lo tanto cuando se tiene una sobretensión de 1.85 pu el valor de la tensión de fase resulta 1.85 ´
429 = 793 kV.