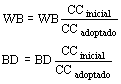Para las armónicas el factor de distribución se da en valor relativo respecto del valor correspondiente a la fundamental, y el orden de la armónica:
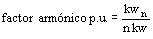
El contenido de las armónicas de un devanado concéntrico puede considerarse bajo, como se observa en la tabla 7.4.
También se nota que para diferentes números de ranuras por polo, ciertas armónicas tienen el mismo valor en p.u. para las distintas distribuciones. A estas se las denomina armónicas de ranura, sólo dependen del número de ranuras por polo, no de la distribución.
En función del número de ranuras por polo la tabla 7.4 permite seleccionar aquella distribución que tenga el menor contenido armónico y que deje un número adecuado de ranuras disponibles (indicadas con x) para el devanado auxiliar o de arranque.
Se observa que el número de orden de la primera columna no es correlativo, este número de 1 a 27 corresponde con la tabla incluida en [1], el orden establecido en la tabla 7.4 es para un número de ranuras por polo creciente, las distribuciones 28 en más se han agregado a las propuestas por Veinott. Ademas el orden de los arrollamientos en la tabla es en base a valores de kw decrecientes para cada grupo con un mismo número de ranuras utilizadas, de manera que cuando el programa adopta un arrollamiento es con el criterio de obtener el mayor kw.
Como antes dicho, durante la ejecución del programa pueden proponerse otras distribuciones cualesquiera y el programa calculará los kw correspondientes debiendo juzgarse estos resultados.
La figura 7.3 muestra los valores de la tabla 7.4, y resulta de utilidad para visualizar rápidamente, en función del número de disposición de devanado, el valor del factor de distribución y el contenido armónico (3, 5, 7, 9, 11 y 13), observándose que prevalece la 3ra. armónica (para algunas disposiciones) y mientras que las restantes se mantienen dentro de una banda relativamente estrecha.
Se han determinado entonces en p.u. los factores de distribución para la fundamental, y para las armónicas impares de interés, también se determinan la suma de cuadrados de los factores de las armónicas y la raíz de esta suma (valor eficaz), que es una forma de totalizar el efecto de las armónicas.
De la expresión del flujo por polo en función de la tensión, se determina el número teórico de conductores activos del devanado.
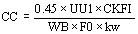
siendo:
CC
: número teórico de conductores activos
UU1
: tensión nominal (V)
CKFI
: factor que afecta la tensión (CKFI = 1 - CIV)
CIV
: caída de tensión relativa
F0
: frecuencia
kw
: factor de distribución de la fundamental
El número de conductores por vía debe ser forzado a un valor compatible con la solución que finalmente se elija, como a continuación se explica, en consecuencia se deberá ajustar el flujo y la inducción en el diente previamente adoptada.
El número de conductores base en la ranura (para CIP = 1) resulta:
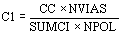
Debiendo hacerse este valor entero, y al menos igual a 1.
El número de conductores en cada ranura se determina con:
Al menos en una ranura se presenta el valor máximo, también se hace la suma de estos valores obteniéndose un nuevo CC = SUMC total de conductores
Se ajusta ahora el flujo por polo y la inducción en el diente, utilizando el valor de CC finalmente adoptado mediante:
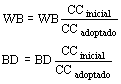
A modo de ejemplo la figura 7.4 muestra el desarrollo del arrollamiento principal o de trabajo a estrato único de un motor monofásico que tiene 18 ranuras estatóricas y 2 polos.
Corresponde a la distribución N°
14 de la tabla 7.4, pudiendo observarse que de las 9 ranuras por polo, 3 están completamente libres para el devanado auxiliar o de arranque. Se representa además el correspondiente diagrama de f.m.m. con la distribución de conductores en las ranuras que se explica a continuación.
También podría haberse elegido la distribución N°
10, observándose aquí que 4 ranuras están disponibles para el devanado auxiliar.
Observemos una diferencia importante, la distribución N°
10 es de paso entero, mientras que la N°
14 es de paso acortado (en una ranura).
Al utilizar la distribución N°
10, de paso entero debe observarse que las ranuras 1 y 10 están compartidas por las bobinas de máximo paso de polos contiguos.
En rigor entonces las ranuras 1 y 10 se encontrarán ocupadas por conductores de dos bobinas de polos distintos, para estas encuentran sentido los valores BCP que valen 2 para las ranuras compartidas.
Para el ejemplo de distribución N°
14 el número de conductores activos totales resulta CC = 400, el número de vías externas se adopta igual a 1, (los dos polos en serie) y por lo tanto la totalidad de conductores activos (los 400) se deben distribuir debajo de los dos polos (200 en cada polo).
De la tabla se tiene que la distribución en las ranuras de los conductores por polo es proporcional a 2,2,1,0,0,0,1,2,2, el número de conductores por polo entonces debe ser múltiplo de 10, número obtenido sumando los factores de distribución, si el número de conductores por polo no cumple esta condición deberá forzarse.
Por lo tanto el número de conductores activos por ranura resulta C0 = 200 / 10 = 20 para aquellas ranuras que le corresponde el factor 1.
La cantidad de conductores en cada ranura es igual a C0 por el factor de distribución Ci que le corresponde, es decir, C1 = C2 = 2´
20 = 40; C3 = 1´
20 = 20.
En cambio si el número de vías de corriente se adopta igual a 2, el número de conductores activos totales por rama debe ser el mismo, y se deben distribuir debajo de un polo solamente, el número de conductores activos por ranura resulta entonces C0 = 400 / 10 = 40 para las ranuras que les corresponde factor 1 y 80 para las otras.
En este caso el número de conductores por ranura resulta igual al doble de los que se tenían cuando se adoptaba una sola vía externa, siendo la sección igual a la mitad por conducir sólo el 50% de la corriente.
En los devanados concéntricos (normalmente utilizados en este tipo de motores) no hay un paso único de bobina, como para los devanados a doble estrato utilizados en máquinas trifásicas, pudiéndose definir un paso promedio como si todas las bobinas fuesen iguales, y que se utiliza en los cálculos donde interviene la dimensión de la bobina.
Para la distribución adoptada el programa construye una tabla que muestra el factor CIP de distribución de conductores por ranura, el factor de multiplicidad BCP que es 1 cuando la ranura no se comparte y 2 cuando se comparte y finalmente los pasos para cada una de las bobinas que forman el arrollamiento principal.
A continuación se indica la suma de los factores de distribución, el factor de distribución para la fundamental y los factores armónicos en p.u. para los armónicos considerados.
El paso promedio se calcula en función del número de conductores alojados en cada ranura y del paso que tiene cada una de las bobinas que componen el arrollamiento con la expresión:
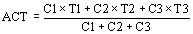
donde para el primer ejemplo considerado el número de conductores efectivos por ranura es C1 = C2 = 40 conductores, C3 = 20 y los pasos de cada bobina son T1 = 8, T2 = 6 y T3 = 4, obteniéndose ACT = 6.4.
Tampoco hay una longitud única de cabeza de bobina y se define en modo análogo una longitud promedio que es igual al producto del arco que corresponde al diámetro en el centro de las ranuras estatóricas multiplicado por una constante empírica y por el paso promedio.
La longitud media del conductor utilizada para los cálculos resulta entonces:
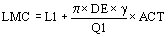
siendo:
DE
: diámetro en el centro de las ranuras del estator
g
: 1.3 para 2 polos, 1.5 para 4 polos y 1.7 para 6 o más polos.
Se impone para este devanado la densidad de corriente en consecuencia se obtiene la sección del conductor y su diámetro (téngase en cuenta que para estos motores se utilizan conductores de sección redonda), y se ajusta el diámetro a valores normalizados, se recalcula el área y la densidad de corriente.
En el cuarto paso se determina a partir de la corriente, densidad de corriente, y número de vías, la sección de los conductores y su diámetro. Si este último no fue impuesto se adopta el valor calculado, en caso contrario a partir del diámetro impuesto se determinan los valores de interés.
Se determina el área neta ocupada por el máximo número de conductores por ranura y el coeficiente de aprovechamiento. Nótese que todavía no se tiene en cuenta el bobinado de arranque.
Con el peso específico se determina el peso total de este arrollamiento, y con la resistividad su resistencia y la caída relativa de tensión que se compara con el valor previamente adoptado.
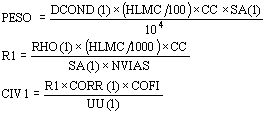
siendo CIV1 la componente resistiva de la caída de tensión.
Característica magnética utilizada para los cálculos
El decimotercer registro incluye los siguiente datos:
relleno
(dato nulo)
SHEL
: paso de hélice del rotor
FREBW
: frecuencia de referencia de inducción pérdidas
EBW
: exponente de la característica inducción pérdidas
relleno
(dato nulo)
CSF
: coeficiente de pérdidas superficiales (para el material magnético utilizado por el programa vale 1.85).
En el quinto paso se determinan las pérdidas y la corriente de excitación.
El decimocuarto incluye los siguientes datos:
BW
: hasta 8 valores de inducción ordenados en forma creciente
El decimoquinto:
WK
: hasta 8 valores de las correspondientes pérdidas en W/kg
El decimosexto:
AS
: hasta 8 valores de las correspondientes intensidades de campo en A/cm.
Si estos datos son nulos, el programa carga los correspondientes al material grado 2 de bajo contenido de carbono de la figura 7.5 que corresponde a una característica magnética de material estándar usado para motores de inducción en la bibliografía [1].
La curva de magnetización que se extrae de los catálogos, es aplicable cuando se tiene una distribución de la inducción uniforme (como por ejemplo en un transformador), en cambio no es aplicable cuando la inducción no es uniforme en las distintas partes del circuito magnético como ocurre en un motor.
Es necesario para calcular obtener una característica magnética que tenga en cuenta esta situación.
El valor máximo de inducción en los dientes se tiene en el centro de un polo, para los restantes dientes se considera que la inducción varía con ley sinusoidal como se indica en la curva Bd de la figura 7.6.
Con los valores de inducción en los distintos puntos (dientes) y con la curva de saturación figura 7.5 se obtienen los correspondientes valores de f.m.m. y se construye la curva de f.m.m. indicada en la figura 7.6, que muestra un pico más o menos pronunciado función del valor máximo de inducción.
La curva que corresponde a la f.m.m. encierra un área (integral a lo largo de un polo), a los fines del cálculo se puede suponer una fuerza magnetomotriz equivalente que tiene distribución sinusoidal y que encierra la misma área.
En consecuencia algunos dientes tendrán f.m.m. en exceso otros en defecto y en promedio el valor de la fuerza magnetomotriz equivalente será representativo en modo aceptable para el cálculo.
Repitiendo este análisis para distintos valores de inducción en los dientes en correspondencia con el eje de simetría del polo (inducción máxima), se obtiene una curva de magnetización ponderada como muestra la figura 7.7 que es utilizada en los cálculos.
El programa determina esta característica a partir de la curva de magnetización entrada como dato.
La integral de la curva Bd corresponde al flujo que se establece en los dientes correspondientes a un polo, y que debe conducirse por la corona tanto del estator como del rotor.
La integral de esta curva tiene una variación cosenoidal que tiene valor cero en el centro del polo y máximo en ambos extremos.
Suponiendo que el valor de inducción máximo en la corona es el mismo que para los dientes (en los motores reales siempre es menor), los valores de f.m.m. para esta parte del circuito varían punto a punto como para los dientes.
Se toma como f.m.m. ponderada para la corona tanto del estator como del rotor, el valor medio del valor pico correspondiente a la curva de f.m.m. equivalente, es decir, para la corona se multiplica por 2/p
los valores de la curva de saturación ponderada.
Factores de Carter y de flujo
En el sexto paso se calculan los factores de Carter para el estator y el rotor, su producto y además otros factores que se explican a continuación.
En máquinas monofásicas (también se utiliza en las polifásicas) se define el factor KP denominado factor primario del flujo que tiene en cuenta la impedancia de magnetización (reduce el flujo)
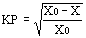
siendo X0 la reactancia de dispersión de vacío y X
la reactancia de dispersión de cortocircuito.
Este factor KP se lo utiliza para calcular las inducciones en la corona, en el diente del rotor y en el entrehierro.
Como todavía no se han determinado las reactancias, se pude estimar su valor con la expresión
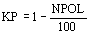
donde NPOL es el número de polos.
En máquinas monofásicas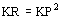 
es el factor total del flujo que se utiliza para calcular la inducción en el entrehierro.
El flujo en el rotor es menor que el del estator, debido al flujo disperso en el estator, en máquinas monofásicas el flujo se reduce aún más que en las polifásicas, y se tiene en cuenta este efecto mediante el factor de flujo KC que se utiliza para calcular la inducción en la corona y en el diente del rotor.
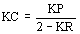
Se calcula, como ya visto para el motor asincrónico trifásico, el valor de inducción en cada tramo del circuito magnético (estator, rotor y entrehierro).
Con estos valores utilizando la curva de magnetización ponderada se determina la tensión magnética necesaria para cada tramo del circuito (dientes y corona) de estator y la tensión magnética total. También se determinan las pérdidas especificas, las parciales correspondientes y las totales del estator.
Finalmente si corresponde se deben corregir las pérdidas en relación con la frecuencia de funcionamiento del motor, y de las características magnéticas, según se indica:
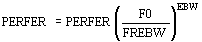
El cálculo se repite para el rotor, pero solo se determina la tensión magnética.
Se calcula el factor de saturación como relación entre la f.m.m. total (incluyendo la corona y dientes del estator y del rotor) y la f.m.m. del entrehierro. Se destaca que el cálculo de este factor se diferencia del utilizado para el motor polifásico, donde no se considera la corona del estator y del rotor.
(Wb)
