CAPITULO 13
ESFUERZOS DE CORTOCIRCUITO EN TRANSFORMADORES
Por
Ings. Jorge N. L. Sacchi – Alfredo Rifaldi
Introducción
Cuando ocurre un cortocircuito en una red, las corrientes de cortocircuito que circulan por los arrollamientos de un transformador los someten a esfuerzos.
Esta situación también se presenta cuando en un laboratorio de pruebas se reproducen las mismas condiciones de funcionamiento.
Los esfuerzos que se presentan se distinguen en térmicos y electrodinámicos.
Los efectos térmicos pueden evaluarse por medio de cálculo. Las normas fijan criterios para determinar la temperatura máxima que alcanza el conductor.
Los esfuerzos electrodinámicos son consecuencia de la coexistencia de las elevadas corrientes, con el campo magnético de dispersión y alcanzan valores elevados que pueden llevar el transformador al colapso, su rotura.
La importancia del problema, por sus consecuencias crece con la potencia de la máquina. Debe destacarse que la reducción de la tensión de cortocircuito es un factor que incrementa también la importancia de estos fenómenos.
Los ensayos de transformadores pueden ser ejecutados en laboratorios muy especializados cuyo número se reduce a medida que la potencia nominal del transformador crece.
La dificultad de hacer ensayos y el costo que estos tienen, ha impulsado el desarrollo de métodos de cálculo para juzgar el comportamiento de los transformadores bajo esfuerzos electrodinámicos.
Determinación de la corriente de cortocircuito
Para observar los efectos de la corriente de cortocircuito es necesario encontrar el valor representativo, se considera que este debe ser el valor máximo que puede presentarse.
Este valor surge de la tensión de alimentación, de la impedancia de la red y de las características del transformador.
La norma IEC 76-5 fija los valores de impedancia para distintos rangos de potencia de un transformador; si se trata de un transformador calculado el valor de la impedancia es conocido.
Tabla I - Valores característicos de la impedancia de cortocircuito para transformadores de dos arrollamientos
|
Potencia
KVA |
Impedancia
% |
|
Hasta 630 |
4.0 |
|
631 a 1250 |
5.0 |
|
1251 a 3150 |
6.25 |
|
3151 a 6300 |
7.15 |
|
6301 a 12500 |
8.35 |
|
12501 a 25000 |
10.0 |
|
25001 a 200000 |
12.5 |
También fija para la tensión más alta del sistema la potencia de cortocircuito en el punto de alimentación del transformador.
Tabla II - Potencia de cortocircuito aparente de un sistema
|
Tensión máxima del sistema
kV |
Potencia aparente de cortocircuito MVA |
|
7.2, 12, 17.5 y 24 |
500 |
|
36 |
1000 |
|
52 y 72.5 |
3000 |
|
100 y 123 |
6000 |
|
145 y 170 |
10000 |
|
245 |
20000 |
|
300 |
30000 |
|
420 |
40000 |
En base a la tensión máxima del transformador se determina la potencia de cortocircuito de la red suponiendo que se lo alimenta desde este lado.
Se debe calcular la potencia de cortocircuito (corriente) para el cortocircuito del lado contrario al devanado de alimentación
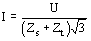 kA
kA
donde:
U:
tensión máxima, o nominal según se desee lado alimentación kV
Zs = Umax12 / Pcc
la impedancia de la red
Zt = Ucc ´
Un12 / (100´
POTKVA / 1000)
la impedancia del transformador referida a la red (Ucc es la impedancia del transformador, Un1 la tensión nominal, POTKVA la potencia)
Estos cálculos deben ser ejecutados teniendo en cuenta las componentes resistivas y reactivas de cada impedancia.
El valor de pico de la corriente de cortocircuito se determina en base al factor que se obtiene de la tabla V y es función de la relación X/R.
Tabla V - Valores del factor k y kÖ
2
|
X/R |
1 |
1.5 |
2 |
3 |
4 |
5 |
6 |
8 |
10 |
³
14 |
|
k |
1.07 |
1.16 |
1.24 |
1.38 |
1.48 |
1.55 |
1.61 |
1.68 |
1.74 |
1.80 |
|
kÖ
2 |
1.51 |
1.64 |
1.76 |
1.95 |
2.09 |
2.19 |
2.27 |
2.38 |
2.46 |
2.55 |
hechas estas determinaciones se dispone de todos los valores que caracterizan la corriente de cortocircuito.
Determinación de la temperatura máxima del conductor
Se puede suponer que antes del cortocircuito el transformador se encuentra en su condición de carga nominal.
Como la norma fija algunas condiciones límites, se puede suponer que la temperatura inicial del devanado es la ambiente (40 °C) más la sobreelevación del conductor correspondiente a la clase de aislación (para Clase A por ejemplo 65 °C) y el objetivo del cálculo es determinar la temperatura final para cierta duración de la corriente de cortocircuito.
La temperatura final J
1 de acuerdo con la IEC 76-5 Amend 2 @ (1994) resulta:
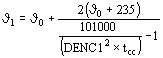 °C (cobre)
°C (cobre)
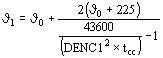 °C (aluminio)
°C (aluminio)
siendo:
J
0:
temperatura inicial del conductor
DENC1
: densidad de corriente en cortocircuito A/mm2
tcc
: duración del cortocircuito seg.
Estos cálculos deben realizarse para cada uno de los distintos devanados, debiéndose controlar finalmente que no se excedan los valores de J
2.
Tabla III - Valores máximos de la temperatura media de devanados después de un cortocircuito J
2
|
Tipo de transformador |
Temperatura de la clase de asislación |
Valor de J
2 |
| |
|
Cobre |
Aluminio |
|
Inmerso en aceite |
A |
250 °C |
200 °C |
|
Secos |
A
E
B
F y H |
180 °C
250 °C
350 °C
350 °C |
180 °C
200 °C
200 °C
¾
|
Por razones didácticas, y siendo un antecedente de interés que se utilizó durante varios años se transcribe la modalidad indicada en la IEC 76-5 (1976).
La temperatura final J
1 es:
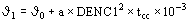 °C
°C
siendo:
J
0
: temperatura inicial del conductor °C
DENC1
: densidad de corriente en cortocircuito A/mm2
tcc
: duración del cortocircuito seg.
a
: factor auxiliar
La densidad de corriente que interesa para el cálculo es la que corresponde al arrollamiento en cortocircuito que se analiza, y puede obtenerse a partir de la densidad de corriente correspondiente a la potencia nominal por la relación entre la corriente nominal y la de cortocircuito.
Según el material con que está construido el devanado cobre o aluminio, se determina un factor auxiliar que depende del calor específico, densidad y resistividad, que varía con la temperatura.
Este factor se encuentra en la tabla IV de la norma, y es función de la temperatura media J
m y del material.
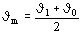 °C
°C
La Tabla III fija los valores máximos permisibles de J
L según el tipo de transformador, clase de aislación y material del conductor.
Para calcular el valor de "a" es necesario conocer J
1 temperatura final que es incógnita, esto puede hacerse en forma iterativa, partiendo de un primer valor de J
1 se determina a y con él se calcula un mejor valor de J
1 hasta lograr un resultado satisfactorio.
Este cálculo supone que el proceso de calentamiento del conductor durante el cortocircuito es un fenómeno adiabático, es decir que todo el calor producido por la corriente incrementa la temperatura del conductor
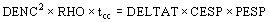
siendo:
DELTAT
: incremento de temperatura por la corriente de cortocircuito
CESP ´
PESP
: calor especifico por densidad
DENC
: densidad de corriente A/mm2
RHO
: resistividad media para el salto de temperatura W
mm2/m
tcc
: duración del cortocircuito seg
El valor de J
1 no debe superar los límites de la tabla III según el tipo de transformador, clase de aislamiento y material conductor.
Otro problema puede ser determinar la duración del cortocircuito que haga se alcance la temperatura límite, en este caso el cálculo es inmediato.
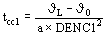 seg
seg
Esfuerzos electrodinámicos
Para que un transformador sea capaz de superar con éxito los esfuerzos de este tipo que se pueden presentar durante su vida, es necesario:
- verificación por medio del cálculo y de ensayos;
- un adecuado programa de control de calidad de los materiales utilizados;
- y control del proceso de fabricación de los componentes y de su montaje.
Se destaca que sólo el buen diseño y verificación de cálculo no dan suficiente garantía, son indispensables por ejemplo el control de las características físico químicas de los materiales conductores y aislantes, el control de fabricación de los arrollamientos durante su elaboración y armado final, y de los procesos de secado, estabilización, impregnación, etc. y finalmente proceder a un adecuado mantenimiento.
En este trabajo se describe una metodología simplificada para calcular las solicitaciones de los arrollamientos sometidos a estos esfuerzos.
Además se señala la orientación para efectuar estudios más rigurosos para mejorar el conocimiento de estos fenómenos y evaluar cuantitativamente sus consecuencias.
Los ensayos de laboratorio son los que finalmente permiten verificar la validez de los modelos adoptados en los cálculos, y en consecuencia realimentar la experiencia de quien realiza este tipo de trabajos.
Las normas también establecen las condiciones que deben cumplir los transformadores con relación a estos ensayos.
Es necesario disponer de métodos de cálculo por lo siguiente:
- como medio de comparación entre valores calculados y resultados de ensayo
- para los casos en que no es posible efectuar ensayos de cortocircuito, es decir sobre todo para transformadores mayores que las posibilidades de ensayo
Características mecánicas de los materiales conductores
Los materiales normalmente utilizados en la construcción de los devanados de los transformadores son el cobre y el aluminio, estos materiales pueden ser recocidos o endurecidos por elaboración en frío.
Las normas indican para cada tipo de material los valores de resistividad que no deben superarse para una temperatura de referencia, para garantizar la calidad del material.
El módulo de elasticidad E y la carga límite de fluencia s
D son las características que se requieren conocer para la determinación de la resistencia mecánica de los metales a esfuerzos.
La característica deformación en función de la carga para el cobre y el aluminio se apartan gradualmente de la linealidad, no estando bien definidos los límites de proporcionalidad y de fluencia (como ocurre con el hierro).
Por esta razón se adopta como límite de fluencia la carga para la cual corresponde una deformación permanente igual a 0.2 % de la longitud inicial de la probeta, y se lo denomina s
0.2 (kg/mm2).
La deformación está dada por la relación
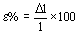
y el módulo de elasticidad
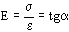
La figura 1 muestra el significado de estos parámetros.
El límite de fluencia está relacionado con los siguientes factores:
a. Endurecimiento debido a la elaboración en frío. En estas condiciones para el cobre el valor de s
0.2 puede ser aumentado de 4 kg/mm2 (material recocido) hasta 40 kg/mm2, análogamente para el aluminio se pasa de 1.8 kg/mm2 a 17 kg/mm2.
b. El valor de s
0.2 disminuye con el aumento de la temperatura, por ejemplo pasando de 20 °C a 105 °C se tiene una reducción del orden del 10 %.
c. La aleación con otros metales (por ejemplo un 0.04 % de plata en el cobre, para el aluminio el contenido de cobre no debe ser mayor de 0,05 % y de cobre más silicio más hierro no mayor de 0,5 %) puede mejorar s
0.2 sin empeorar la conductibilidad.
Características mecánicas de los materiales aislantes
Los materiales aislantes más utilizados en la elaboración de los devanados de grandes transformadores son el papel tipo kraft con una densidad del orden de 0.75 a 0.85 kg/dm3, con espesor típico de 0.5 mm, y el transformerboard para la elaboración de cilindros de soporte, distanciadores, listones separadores etc. es normalmente de tipo duro, prensado en caliente, con una densidad del orden de 1.25 kg/dm3 y distintos espesores.
En máquinas de menor tamaño se usan otros materiales aislantes de menor jerarquía, y la madera.
Puesto que los conductores son mucho más rígidos que el papel y el transformerboard el comportamiento de los arrollamientos sometidos a las fuerzas axiales de cortocircuito está definido por la respuesta de los aislantes a los esfuerzos de compresión.
En los diagramas de deformación en función de la carga, que representan la característica mecánica más importante de los aislantes, se puede observar como se comportan y evaluar su conducta frente a un cortocircuito.
Al examinar estos diagramas es necesario considerar los casos de carga estática y dinámica.
Carga estática
Se presenta cuando un arrollamiento se somete a la compresión constante o bien variada pero en forma relativamente lenta. Esto ocurre durante el tratamiento y montaje de los arrollamientos.
Si un arrollamiento estabilizado (sometido en forma lenta a la compresión y secado antes de ser montado), se lo somete a ciclos sucesivos durante los cuales la presión supera el valor máximo de estabilización, se verifican ulteriores deformaciones permanentes y es necesario repetir 3 a 4 ciclos para obtener una nueva estabilización.
El estado en cual queda el arrollamiento que ha sido sometido a este tratamiento se lo denomina precompresión.
La determinación de las características mecánicas de los materiales aislantes, es decir, la característica deformación en función de la carga, es un problema muy importante. Los resultados obtenidos por distintos investigadores son bastante discordantes.
Estas diferencias se deben al hecho que los resultados experimentales dependen de numerosos factores, siendo los más importantes:
- El tratamiento preliminar del prototipo (presión, temperatura, etc.)
- Dimensiones del prototipo y cantidad de capas
- Terminación de la superficie
- Duración de aplicación de la carga
- Temperatura de la prueba
Si se dispone de los diagramas para el papel e
1 = f (s
) y para el transformerboard e
2 = f (s
) se puede durante el proyecto estimar las deformaciones estáticas de un devanado cualquiera.
Siendo en efecto los conductores mucho más rígidos que los materiales aislantes, su deformación se puede despreciar y por lo tanto para la deformación de un devanado sometido a la compresión se tiene:
D
H = D
H1 + D
H2
siendo D
H1 y D
H2 la deformación del papel y del transformerboard respectivamente.
Por otro lado se tiene:
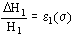
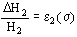
donde H1 y H2 son el espesor total de papel y el espesor total de transformerboard en el sentido axial del arrollamiento.
Para un valor de la carga s
de los diagramas correspondientes se tienen los valores de e
1 y e
2 y con ellos se calcula el valor de la deformación total del devanado.
Para tener una cierta precisión se debe tener en cuenta para el cálculo de D
H la disminución de volumen debido al proceso de secado, las deformaciones permanentes provocadas por los ciclos de estabilización y el efecto de rozamiento.
Carga dinámica
La carga dinámica se presenta durante el cortocircuito de un transformador, también cuando se producen sobrecargas de importancia y durante una energización (corriente de inserción).
Los conductores del devanado están sometidos a una fuerza mecánica que es proporcional al cuadrado de la corriente, que se tiene en el caso más desfavorable (máxima asimetría).
Las figuras 2 y figura 3 muestran la variación de la corriente y de las fuerzas actuantes en función del tiempo, observándose en la corriente la componente unidireccional (continua), que se extingue en breve tiempo.
Para las fuerzas (supuestas proporcionales al cuadrado de la corriente) existen dos componentes variables, una de la misma frecuencia que la corriente que desaparece con la componente continua, y la otra permanente con frecuencia doble.
Estas componentes aplicadas sobre los conductores provocan esfuerzos y vibraciones.
Esfuerzos, y vibraciones pueden presentarse en forma radial y axial.
El análisis de las vibraciones axiales se puede realizar considerando un sistema de masas y resortes como se indica en la figura 4. Las masas representan los conductores y los resortes los aislantes.
La representación de los materiales aislantes con resortes es posible aunque ellos sólo pueden transmitir esfuerzos de presión y no de tracción, porque los arrollamientos están sometidos a una cierta presión de sujeción que da un estado de precompresión.
Entonces las vibraciones de los conductores provocan aumentos y reducciones de la compresión de los aislantes sin solicitarlos a la tracción.
Si en algunos puntos del arrollamiento la reducción de la presión supera el valor de la compresión se producen separaciones entre conductores y distanciadores.
Para evaluar la respuesta del sistema vibratorio a las fuerzas de cortocircuito, es necesario conocer la característica de los resortes, es decir los diagramas de deformación en función de la carga de los aislantes en condiciones dinámicas.
Estos diagramas no son lineales y no son iguales a aquellos obtenidos para las cargas estáticas.
La figura 5 muestra que por encima del punto de precompresión, en condiciones dinámicas el transformerboard es más rígido y se deforma menos, por debajo de este punto no hay diferencias entre ambas condiciones.
La explicación del comportamiento dinámico del transformerboard se debe a que cuando se le aplica improvisamente una fuerza, el aceite contenido en sus poros está sometido a una presión y tiende a salir. El recorrido del aceite es a través de una estructura capilar y se realiza en forma lenta, por lo tanto durante el tiempo breve transcurrido hasta que la fuerza alcanza su primer pico, el aceite queda atrapado y debido a su alta constante elástica confiere rigidez al transformerboard.
Cuando en cambio la fuerza aplicada reduce la precompresión la presión del aceite retorna al valor inicial, y como no puede transmitir esfuerzos de tracción, la rigidez es solamente la propia del transformerboard.
Se supone que la principal flexibilidad del sistema corresponde al transformerboard (y el papel, pero su influencia es mucho menos importante que la del transformerboard puesto que los espesores de papel son relativamente pequeños).
![]() kA
kA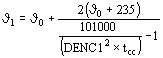 °C (cobre)
°C (cobre)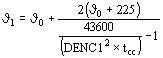 °C (aluminio)
°C (aluminio)