El estudio de las máquinas eléctricas, y en particular cuando se intenta profundizar sus características y su funcionamiento, debe encararse en la dirección de los campos, y no solo eléctricos y magnéticos.

Merece tenerse siempre presente que G. M. Pestarini, en 1943, inició su libro "Elettromeccanica" destacando la importancia de estos temas, con las palabras cuya traducción libre sigue:

Y estas palabras que resonaron en un aula hace más de 50 años son motivo más que suficiente para que observemos algunos temas ligados a la construcción y utilización de máquinas desde esta óptica.

El estudio de los campos nació de la observación experimental de ciertos fenómenos, el fluir del agua del río, la orientación de limaduras de hierro, que generaron la comprensión de las razones físicas de las formas de los campos, interviniendo finalmente las matemáticas que propusieron las ecuaciones diferenciales que los explican.

Además la analogía entre distintos campos permite aplicar la teoría de la semejanza, transfiriendo conocimientos de un área de la física a otra.

Parece lógico siendo nuestra especialidad la eléctrica, orientar el estudio a partir de los campos eléctricos y magnéticos, y transferir estos conocimientos a los otros temas de interés en las maquinas eléctricas, más en general a las distintas ramas de la electrotecnia.

El libro seleccionado para usarlo de guía en el estudio es el de John D. Kraus, "Electromagnetismo" (Mc Graw Hill), y seguimos el orden en el establecido.

Inspiración del enfoque de varios puntos ha sido el ya viejo libro de G. M. Pestarini, Elettromeccanica Volume I "Fondamenti di costruzione comuni a tutte le macchine", también hemos utilizado el libro de Antonio Carrer "Note di Elettrotecnica, indirizzo Correnti Forti" que dedica medio volumen a estos temas, evidenciando su importancia.

Una advertencia, al estudiar estos temas, las herramientas matemáticas son de extraordinaria ayuda, pero pueden hacer perder el sentido físico de los temas que se pretenden analizar, para evitar esto se ha hecho el intento de orientar el trabajo exclusivamente hacia los conceptos físicos, ninguna demostración matemática se ha incluido.

El lector debe aportar su conocimiento de matemática, y si nota su falta, a estudiar para lograr el adecuado soporte, encontrar las demostraciones, entender mejor las cosas, pero en ningún momento perder el sentido físico de lo que se esta analizando.

Entre dos cargas eléctricas se presenta una fuerza (Fig. A1.1):

(1)

siendo:

F: fuerza en (N)

r₁: vector unitario (versor) en dirección de la recta que une las cargas, y que da sentido a la fuerza

Q₁, Q₂: cargas eléctricas puntuales (Culomb)

e ₀: permitividad del vacío = 8.859 ´ 10^-12 (F/m)

r: distancia entre las cargas (m)

Para un medio dieléctrico genérico cualquiera

donde e _r es la permitividad relativa.

El concepto de cargas eléctricas puntuales es ideal, frecuentemente se hacen modelos ideales para simplificar un problema y acercarse a la solución.

Si la carga Q₂ es una pequeña carga de prueba positiva, se define la intensidad del campo eléctrico:

Newton / Culomb = Volt / m (2)

Si la carga Q₁ es positiva, y como la carga de prueba también lo es, las cargas se repelen, la fuerza es en la dirección de la recta que une las cargas, en el sentido de alejarlas, y este es el sentido del campo también.

Si hay varias cargas, que consideradas individualmente en un punto nos dan varios campos, el campo total resultante puede obtenerse por suma vectorial de los campos componentes individuales en cada punto, este es el llamado principio de superposición (Fig. A1.2).

Si la carga de prueba positiva se desplaza, a lo largo de un camino D x, se efectúa cierto trabajo:

F . D x = trabajo sobre Q₂ en Joules o Newton . m

El trabajo por unidad de carga es el potencial eléctrico escalar

volt (3)

El potencial en el infinito es convencionalmente cero, crece en dirección a la carga positiva (Fig. A1.3).

(4)

E y dl son vectores con dirección y sentido, el producto es escalar.

El potencial debido a una esfera cargada Q₁ a una distancia r del centro de la esfera resulta:

(5)

Si se sigue la dirección del campo se traza una familia de líneas de campo, en cada punto se conoce la dirección del campo, si partiendo de puntos próximos se trazan varias líneas se observa que la densidad de líneas es proporcional a la intensidad del campo (Fig. A1.4).

La línea de campo indica la dirección de la fuerza sobre la carga exploradora, si se suelta la carga exploradora (que no tiene masa) esta recorre la línea de campo, en dirección de la línea, hacia los potenciales menores, estas líneas se llaman también de desplazamiento y el flujo de desplazamiento eléctrico.

Las líneas equipotenciales son normales a las líneas de campo, en efecto si la fuerza es normal al camino no se hace trabajo (se conserva el potencial).

Se recomienda la lectura de John D. Kraus, Electromagnetismo (Mc Graw Hill) sección 2-9 Relación entre líneas del campo eléctrico y contornos equipotenciales; ortogonalidad.

Conviene observar campos producidos por cargas, para fijar los conceptos, veamos entonces:

En este caso obsérvese el campo no uniforme en proximidad de la carga puntual, las líneas de campo divergentes de la carga, las superficies equipotenciales que a medida que nos alejamos de la carga están cada vez más alejadas entre si.

Obsérvese en estos casos que el campo es simétrico respecto del plano de simetría de las cargas, una mitad del campo espacial es imagen especular de la otra mitad, de aquí comienza a intuirse el método de las imágenes, en un caso imagen de igual signo, y de distinto en el otro.

Para el caso de signos iguales se destaca la línea equipotencial que se cruza sobre sí misma, donde el campo es nulo.

El punto donde el campo y las líneas equipotenciales no son perpendiculares se llama singular.

Para el caso de signos opuestos además obsérvese el campo en una pequeña región en el centro sobre el eje que une las cargas, en esa zona el campo es uniforme, en la proximidad de las cargas no.

Hasta ahora hemos pensado en cargas puntuales, pensemos ahora en distribuciones continuas de carga:

r = Q / v densidad volumétrica de carga

r _s = Q / s superficial (característica en la superficie de conductores)

r _L = Q / l lineal

Como para el campo eléctrico el potencial eléctrico con distribuciones de carga, se determina aplicando el principio de superposición (del potencial). El potencial eléctrico total en un punto es la suma algebraica de los potenciales individuales en el punto.

(6)

y para distribuciones continuas la sumatoria se reemplaza por la integral

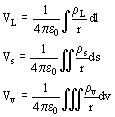(7)

Observemos una carga lineal indefinida, pensemos se trata de cargas r _L . dl, que desde cierta distancia parecen cargas puntuales (fórmula 2), determinamos el campo en una superficie normal a la línea de carga, aplicando superposición

(9)

No debemos olvidar que E es un vector, con dirección r, por lo que si deseamos resultados escalares debemos integrar sus componentes, según una línea paralela a la línea de carga y otra paralela a la normal, la integral se debe extender entre los límites - µ a + µ .

Si el punto en estudio (en la superficie) está a distancia R de la intersección de la superficie con la línea, la distancia r al elemento dl de la línea es:

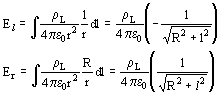(10)

El resultado de la integral que se busca entre los valores de l, límites - ¥ e ¥ :

(11)

También puede ser de interés el resultado del campo que se tiene alrededor de un trozo finito de conductor rectilineo (de longitud dada), eligiendo convenientemente los limites de integración y teniendo en cuenta las proyecciones de E en las tres dimensiones se puede encontrar el campo eléctrico en todo el espacio de interés.

Volviendo al conductor rectilineo indefinido, el campo que se determina es bidimensional, no se distingue entre una superficie normal al conductor y otra.

Vale comparar el campo bidimensional debido al conductor indefinido (punto o círculo en el plano), con el campo tridimensional debido a una carga puntual, (esférica en el espacio), el campo tridimensional varía con la inversa de r² (fórmula 2) , y el campo bidimensional en cambio varía con la inversa de r.

El potencial debido a un conductor rectilineo indefinido se determina integrando el campo eléctrico:

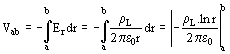(12)

La diferencia con el potencial debido a una carga puntual en el espacio (tridimensional ver fórmula 5) es más notable, el potencial en el infinito (para el problema bidimensional) no puede ser determinado, mientras que lo pudimos adoptar nulo para el problema de la esfera cargada (tridimensional).

Hemos visto la expresión integral del campo, y obtenido el potencial, en consecuencia campo eléctrico es el gradiente del potencial eléctrico.

El operador gradiente se aplica a un escalar (V potencial), y se obtiene un campo vectorial (-E), se convierte una función escalar en otra vectorial, que físicamente están íntimamente relacionadas.

En matemáticas el operador Gradiente se representa con el símbolo griego Ñ nabla.

En coordenadas rectangulares el operador nabla:

Cuando los problemas presentan particulares condiciones de simetría conviene utilizar coordenadas cilíndricas o esféricas, o en general coordenadas curvilíneas, en cada una de ellas el operador es formalmente distinto aunque su significado es único.

Dos cargas iguales de signos opuestos son un dipolo eléctrico, aplicando la fórmula 5 y 6 se obtiene V.

Fijando el origen de coordenadas entre las dos cargas, y reemplazando las distancias r entre carga y punto (de coordenadas r y J ) por una aproximación válida para r >> l se obtiene (Fig. A1.7):

(15)

donde se llama momento del dipolo al producto Q. l.

Se supone que las líneas de campo conforman tubos, que encierran un flujo, cada tubo encierra una cantidad constante de flujo eléctrico (Fig. A1.8).

D = flujo / área (16)

D es la densidad de flujo

en el vacío D = e ₀ . E y en un medio D = e . E (17)

Sobre una esfera de radio r, D es la carga distribuida uniformemente.

El flujo eléctrico a través de cualquier superficie cerrada es igual a la carga encerrada, esta ley se conoce con el nombre de Gauss.

(18)

Los materiales conductores conducen o transportan carga eléctrica. El conductor sumergido en un campo eléctrico se comporta de manera de que el potencial sea uniforme en todo el conductor, y para lograr esto se inducen cargas eléctricas (Fig. A1.9). En el interior de los electrodos la intensidad de campo debe ser nula, si no fuera así no serían equipotenciales.

Volviendo al ejemplo de un trozo de conductor rectilineo, de longitud dada, donde se ha encontrado el campo (fórmulas 10) y puede determinarse el potencial en todo el espacio de interés, se observa (estudiando en detalle) que el potencial sobre el conductor obtenido al resolver el problema no es constante, la física nos señala que el potencial en la superficie del conductor es constante, y para ello la distribución de carga a lo largo del conductor debe ser adecuada, no uniforme, de todos modos en primera aproximación se puede aceptar el resultado ideal obtenido.

Las fórmulas que se aplican para determinar las equipotenciales del campo eléctrico en el plano del espacio que contiene cierta cantidad de cargas esféricas son muy simples (ver fórmula 6) y se trata de un plano que corta cargas cilíndricas paralelas (ver fórmula 12).

Un programa que aplicando estas fórmulas determina el potencial en la zona de interés es fácil de hacer.

Se ha desarrollado "POTESF" que ingresa cierta cantidad de cargas esféricas o cilíndricas (en rigor puntuales) con sus coordenadas y se determina en un área cuadriculada los valores de potencial.

Para cada punto del plano y cada esfera se debe determinar la distancia entre el punto y el centro de la esfera, controlar que el punto es exterior a la esfera y por superposición del valor correspondiente a todas las esferas se determina el potencial, análogamente si se trata de cilindros.

Los resultados obtenidos se vuelcan a un archivo.

El programa "ISOLUX" (indudablemente concebido para otro uso) levantando estos resultados genera las líneas equipotenciales, que podemos observar (Figs. A1.5 y fig. A1.6).

En los resultados se advierten las consecuencias de la hipótesis simplificativa de aceptar asimilar una esfera (o un cilindro) a una carga puntual, el potencial en la superficie de la esfera no es constante, pero es aceptable con cierto error.

Una forma de resolver el problema con exactitud es adoptando una equipotencial como superficie de la esfera (o cilindro) cuyo centro no coincide con la carga puntual.

A modo de ejemplo de los resultados obtenidos con este programa se incluye la (Fig. A1.10) que corresponde a dos dipolos orientados en formas opuestas entre sí y la (Fig. A1.11) con los dipolos orientados en igual forma.