En el cálculo de las máquinas eléctricas los temas de reactancias funcionales de régimen permanente están resueltos en la bibliografía clásica con varias modalidades, obteniéndose resultados razonablemente acertados.

Es más, frecuentemente hay máquinas sincrónicas con una jaula amortiguadora, intuitivamente esta máquina fuera de sincronismo tiene un comportamiento que puede asimilarse al de un motor asincrónico.

Se observan muchos temas, de los que surgen muchas preguntas que merecen respuesta.

Buscando respuestas en la bibliografía, en varias ocasiones nos hemos topado con respuestas que orientan pero no ayudan al cálculo de los parámetros de interés.

Finalmente un artículo de 1958 nos resolvió el problema en detalle, y nos permitió profundizar aún más los temas que siguen.

Quien estudia el funcionamiento de las máquinas sincrónicas en regímenes cualesquiera identifica:

También se trata de determinar constantes de tiempo

El interés en identificar estos valores, señala caminos experimentales, que pueden ser recorridos con independencia del conocimiento de la intimidad de la máquina.

El profundizar estos temas muestra que en general los parámetros tienen distinto valores según se los identifique sobre el eje directo o en cuadratura (transversal).

Deseamos ahora observar estos temas desde el punto de vista del constructor veamos el artículo bibliográfico.

(Traducido por Ing. Jorge N. L. Sacchi y Ing. Alfredo Rifaldi marzo 1998)

Definiciones

Las reactancias, resistencias y constantes de tiempo de máquinas sincrónicas constituyen elementos esenciales que permiten estudiar los diferentes regímenes de funcionamiento de las máquinas.

Es así que gracias a su conocimiento, se pueden determinar las condiciones de funcionamiento no sólo en régimen permanente, sino aún bajo fenómenos accidentales rápidos como: cortocircuito brusco, desconexión de la red, perdida la excitación, etc. Asimismo nos proponemos estudiar las condiciones de funcionamiento en paralelo (ver D 520), evaluar las corrientes de falla y estudiar los regímenes desequilibrados.

Tiene lugar considerar dos categorías de reactancias: las reactancias que se observan según el eje directo (figura 2 - Reactancias según el eje directo) y aquellas que se observan según el eje transversal (dicho igualmente en cuadratura) (figura 3 - Reactancias según el eje transversal). Nosotros distinguiremos dos familias de reactancias con la ayuda de los índices d (directo) y t (transversal) (figura 1- Reactancias de las máquinas sincrónicas).

Según el eje directo nosotros encontramos (figura 2 - Reactancias según el eje directo) x_s reactancia de fuga de inducido; y además el paralelo de:

x_ad reactancia de entrehierro

x_r reactancia de fuga de inductores

x_kd reactancia del circuito amortiguador

Según el eje transversal ahora no encontramos más el arrollamiento inductor, sólo encontramos (figura 3 - Reactancias según el eje transversal):

x_s reactancia de fuga del inducido

x_at reactancia de entrehierro

x_kt reactancia del circuito amortiguador

En régimen permanente, sólo las reactancias x_s y x_ad deben considerarse según el eje directo ellas están en serie su suma define una reactancia llamada sincrónica x_d:

Por analogía según el eje transversal se podrá definir x_t reactancia sincrónica transversal, que es:

El régimen accidental más frecuente es el cortocircuito en bornes en la proximidad de la máquina, de manera que se pueda considerar la impedancia de carga (externa) sobre la cual entrega esta máquina como prácticamente nula.

Recordemos que en todo circuito eléctrico cerrado de resistencia óhmica nula o despreciable, el número de líneas de fuerza que circulan entre inducido e inductor tiende a mantenerse constante. Si e es la fuerza electromotriz de inducido, r su resistencia y L su inductancia se tiene:

Si se cierra el circuito inducido bruscamente sobre una resistencia exterior nula se tiene

y considerando despreciable r resulta

de donde Li = cte

Como L=F /i por definición, F es el flujo que atraviesa el inducido, e i es la corriente se tiene

Diciendo esto en otra forma, al momento del cortocircuito el flujo bruscamente cesa de variar; su eje queda fijo, no gira más junto con los inductores, e induce en estos últimos, como también en el circuito amortiguador si existe, corrientes que son determinadas y se refieren a los diagramas equivalentes de las figuras 4 y figura 5 (Diagramas equivalentes de cortocircuito) con la ayuda de impedancias x_r y x_kd en el eje directo y x_kt en el eje transversal; estas corrientes decrecen siguiendo una ley exponencial dependiente de las constantes de tiempo de los circuitos considerados, las que están condicionadas por las resistencias r_r, r_kd y r_kt.

Se sabe, del teorema de Leblanc, que en el caso de funcionamiento monofásico, el campo que es fijo, puede ser considerado como suma geométrica de dos campos rotantes en sentidos inversos, de amplitudes mitad del campo fijo, una sobre el eje que gira en sincronismo con el inductor la otra en sentido inverso, atravesando continuamente los circuitos de inductor (arrollamientos de excitación y amortiguadores). Nosotros volveremos más adelante sobre este funcionamiento, pero, desde ahora reconocemos que el campo que gira en sentido inverso que el de la máquina provoca la aparición en el inducido de una reactancia suplementaria llamada reactancia inversa y que designaremos x_i.

Cuando el arrollamiento inducido posee un borne neutro se puede definir la reactancia homopolar x₀ que es igual al cociente del término fundamental de una componente homopolar de tensión aplicada entre las fases y el punto neutro por el término fundamental de corriente homopolar que ella determina (i₀).

La reactancia homopolar está muy influenciada por el acortamiento del paso del devanado. Para un acortamiento a = 0.666 las corrientes que circulan en las dos secciones de conductor que implica la ranura son iguales en fase pero en oposición. Se concluye que las fugas en las ranuras en esas condiciones resultan muy pequeñas.

El conocimiento de esta reactancia homopolar es útil en particular para la determinación de las protecciones que se basan sobre el valor de la corriente de falla que circula hacia el neutro.

La reactancia opuesta por una máquina a una variación de la tensión en bornes es función del estado de saturación de su circuito magnético que puede variar, pero sobre todo en el curso del fenómeno estudiado si la variación de tensión es importante.

Salvo convención en contra, las reactancias de una máquina se suponen referidas al estado no saturado. Este es el caso donde las reactancias axiales y transversales de la máquina son independientes.

Sin embargo se deroga esta regla general para definir la reactancia subtransitoria axial x’’_d y la reactancia transitoria axial x’_d las cuales se emplean frecuente en la determinación de las corrientes de cortocircuito bajo tensión normal.

La reactancia transitoria x’_d es igual al cociente de la tensión nominal por el valor inicial de la componente simétrica de la corriente de cortocircuito brusca bajo esa tensión, valor de corriente disminuido en el término del decremento muy rápido subtransitorio y vectorialmente de la corriente preexistente.

La reactancia subtransitoria x’’_d es igual al cociente de la tensión nominal por el valor inicial de la componente simétrica de la corriente de cortocircuito brusco bajo esta tensión, deducción hecha vectorialmente de la corriente preexistente. La máquina está inicialmente en vacío o en régimen nominal, siguiendo una convención definida en cada caso.

La saturación del circuito magnético puede entonces ser apreciada y tiene lugar aplicar un factor de corrección (ver D 480).

El funcionamiento fuera de sincronismo puede ser debido a un mal acoplamiento (paralelo), una sobrecarga, una baja tensión (o de las dos causas últimas simultáneas) provocando una desconexión. En el funcionamiento fuera de sincronismo, dos casos pueden ser observados:

Se puede igualmente hacer funcionar momentáneamente una máquina sincrónica en régimen asincrónico, cuando por ejemplo se desea arrancar sobre una jaula amortiguadora un motor sincrónico o un compensador sincrónico o asimismo si se quiere usar un alternador, por este procedimiento, y próximo al sincronismo se efectúa la sincronización al final del arranque (ver D 510 pág. 5).

En el caso más frecuente el circuito de inductor queda cerrado, se tiene el diagrama equivalente de la figura 6 (Diagrama equivalente, fuera de sincronismo, con el circuito inductor cerrado) y es usado para buscar para distintos resbalamientos el valor de la reactancia total.

Las resistencias se hacen muy importantes con deslizamientos pequeños porque se debe dividir su valor por el deslizamiento, entonces aquellas pueden ser despreciadas cuando se presenta un cortocircuito instantáneo, como en ese momento el deslizamiento a continuación de la inmovilización brusca del flujo de estator, es próximo a 1.

Para obtener la impedancia total, sumaremos a la impedancia estatórica definida por r_s y x_s las tres impedancias en paralelo x_ad ;;

Como estas impedancias están en paralelo nosotros pasamos por intermedio de las admitancias, para las cuales los términos reales e imaginarios se suman aritméticamente. Nosotros tenemos:

admitancia de entrehierro

admitancia de la jaula

admitancia de los inductores

La suma de estas tres admitancias Y_rd se obtiene de la forma:

donde:

a suma de partes reales de Y_ad , Y_kd, Y_r

b suma de partes imaginarias de las mismas cantidades.

Retornando a las impedancias tenemos:

Sumando Z_s a Z_rd obtenemos la impedancia total de la máquina que será de la forma Z_d = c + jd donde la magnitud del módulo será

Se deducirá la corriente absorbida por el estator i_s = 1 / Z_d

y el par correspondiente al deslizamiento g considerado

Tenemos una máquina de 570 kW 3000 V corriente nominal 110 A, la reactancia de referencia de la máquina es igual a:

Nosotros vamos a ver luego de los cálculos los diferentes parámetros en valor unitario. Por ejemplo, la reactancia por fase estatórica que es 2.65 W será en valor unitario

x_s = 2.65 / 15.8 = 0.168.

Nosotros hemos por ahora calculado

Calcularemos el punto correspondiente a un resbalamiento de

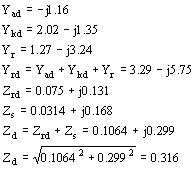
corriente absorbida por el estator:

El par en valor unitario ahora tiene el valor

El par en valor unitario referido al par nominal será entonces:

donde C_N está dado en kgm nosotros obtenemos naturalmente C’ en kgm.

Se puede rehacer este cálculo según el eje transversal a fin de verificar que la corriente absorbida, y el par obtenido son diferentes de aquellos calculados según el eje directo.

En este caso el inductor se comporta exactamente como el rotor de jaula de un motor asincrónico.

Si un alternador se desconecta y si las protecciones interrumpen el inductor, nosotros nos encontraremos en el caso del circuito equivalente (figura 7 - Diagrama equivalente fuera de sincronismo, con el circuito inductor abierto).

El deslizamiento se encuentra entonces muy próximo a 0 al inicio del fenómeno, pues aumenta con la disminución de velocidad de la máquina y se puede tratar el problema como para el circuito de inductor cerrado haciendo simplemente abstracción de la rama r_r x_r.

Desde que se rompe el sincronismo se ve que el eje del inductor se desplaza en relación al eje del flujo estatórico y se debe, para ser riguroso, considerar los diagramas equivalentes sucesivamente según el eje directo y según el eje transversal. Si las impedancias resultantes correspondientes a estas dos posiciones son sensiblemente diferentes, constataremos una pulsación en la corriente que atraviesa la máquina en los dos casos arriba vistos.