Cada una de las corrientes de fase I_a, I_b e I_c (fig. 17 Descomposición de una corriente trifásica asimétrica en componentes simétricas a: sistema de tres corrientes asimétricas) de un alternador sometido a una carga asimétrica cualquiera puede ser considerada como compuesta de tres partes [B 8]

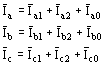
Las corriente I_a1, I_b1 e I_c1 constituyen entre ellas un sistema trifásico simétrico (fig. 17 Descomposición de una corriente trifásica asimétrica en componentes simétricas b: componentes simétricas de sistemas de corrientes) es lo mismo para las corrientes I_a2, I_b2 e I_c2 pero que tienen una sucesión de fases inversa. El sistema de las corrientes I_a1, I_b1 e I_c1 produce un campo que rota en sincronismo con la rueda polar (sistema positivo o directo) mientras que el sistema de corrientes I_a2, I_b2 e I_c2 produce un campo que gira en sentido contrario al de la rueda polar (sistema negativo o inverso). En cuanto a la tercera parte se compone de corrientes iguales I_a0 = I_b0 = I_c0 y sólo se pueden presentar si el punto neutro posee una conexión con el exterior es decir hay un conductor de neutro, en este caso las corrientes I_a0, I_b0 e I_c0 con cada una iguales a un tercio de la corriente en este conductor.

Por esta razón este sistema se denomina sistema homopolar o monofásico (en inglés sistema de secuencia cero).

El sistema directo corresponde a la carga simétrica normal, éstas son las reactancias de las cuales ya nos hemos ocupado, que se tienen en cuenta, ellas son las reactancias sincrónicas X_d y X_q para régimen estacionario y las reactancias subtransitorias y transitorias X’’_d, X’’_q o X’_d para los procesos transitorios.

Supongamos que el sistema inverso sea el único presente. Se tiene entonces en la máquina sincrónica un campo que gira en sentido contrario al de la rueda polar y entonces la velocidad es el doble de la velocidad sincrónica.

De este hecho, la posición del campo rotante varía con el doble de la frecuencia de la red en el eje longitudinal y el transversal.

La reactancia efectiva es así la media de las reactancias longitudinal y transversal medidas a máquina detenida. La reactancia inversa es en consecuencia

En el lugar del símbolo X₂ algunos utilizan el símbolo X_i.

En el sistema homopolar las tres corrientes están en igualdad de fase. No hay ningún campo rotante sino únicamente campos de dispersión. Estos campos dependen mucho de la ejecución del arrollamiento (paso del bobinado, disposición de las cabezas) la reactancia homopolar puede diferir muy sensiblemente aún para máquinas de aspecto análogo.

Los valores varían aproximadamente como siguen:

cuando varios alternadores tienen el punto neutro puesto a tierra trabajando en paralelo, las pequeñas asimetrías son capaces de dar lugar a fuertes corrientes en los conductores neutros. Así no deberá, si es posible, nunca ponerse directamente a tierra el punto neutro de alternadores; al menos por intermedio una reactancia de 10 a 20 % referida a la impedancia nominal del alternador.

Daremos igualmente algunas palabras al respecto de otras reactancias, que son de todos modos mencionadas pero de prácticamente menor importancia que aquellas de las que hasta aquí nos ocupamos.

La reactancia de Potier se determina según la figura 18 (Determinación de la reactancia de Potier con la ayuda de las características medidas) con la ayuda de la característica de vacío U₀ = f(I_e) y de corriente de inductor I_en0 para la corriente nominal y cos j = 0. Ella surge de la determinación aproximada de corriente de inductor y de la variación de tensión para una carga dada según el método ilustrado por la figura 19 (Determinación de la corriente de inductor y de la variación de tensión, con la ayuda de la reactancia de Potier - B 5.9). Una medida directa I_en0 no es siempre posible en el caso de grandes máquinas, y se sirve frecuentemente de valores aproximados para la reactancia de Potier poniendo por ejemplo [B 9]:

o en forma más precisa [B 10]:

donde Xs es la reactancia de fugas de inducido que se puede medir cuando el rotor está fuera de la máquina. A parte el empleo hasta aquí indicado esta reactancia sólo interesa al que calcula.

Como nosotros hemos dicho en el párrafo 4.4, las reactancias sincrónicas X_d y X_q son siempre consideradas por sus valores no saturados.

Cuando los efectos de la saturación juegan un papel importante se introducen en consecuencia valores corregidos. Esto es sobre todo importante para la determinación de la potencia desconectable de una máquina sincrónica y para el estudio de pequeñas oscilaciones. El valor de X_d que interviene para la potencia de desconexión es llamado reactancia equivalente X_eq [B11]. Ella alcanza aproximadamente 0,5 a 0,7 de X_d. Para hablar con propiedad ella no depende únicamente de la máquina sino igualmente en parte de la red conectada.

El comportamiento de máquinas sincrónicas sometidas a pequeñas oscilaciones provenientes de un motor Diesel de impulso, de cargas inestables, o de procesos de regulación, es determinado por las diferentes reactancias que acabamos de describir (X_d, X_q, X’_d, X’’_d, X’’_q) y por las constantes de tiempo correspondientes [B 1].

En numerosos casos el cálculo puede ser todavía simplificado introduciendo la reactancia pendular X¥ [B 12 - 13].

Para ello se sustituye el alternador por una fuerza electromotriz fija E¥ precedida de la reactancia X¥ (fig. 20 - Diagrama vectorial de una máquina sincrónica sometida a pequeñas oscilaciones, para explicar la reactancia pendular) de manera que las oscilaciones de corriente o de la carga sean las mismas que aquellas a las cuales la máquina está sometida.

La reactancia depende entonces en una muy gran medida de la frecuencia pendular. La fig. 21 (Reactancia pendular de una máquina sincrónica con amortiguador completo en función de la frecuencia pendular fp) indica la variación característica de esta relación.

Las máquinas asincrónicas constituyen una parte esencial de la carga de una red, sus reactancias juegan un papel en numerosos casos. Estas máquinas tienen entrehierro constante, y sus arrollamientos simétricos, de manera que ellas no presentan ejes singulares y que todas las constantes son prácticamente independientes de la posición del inducido.

En marcha sincrónica se mide la reactancia en vacío X₀ que corresponde luego a la reactancia X_d. El entrehierro es menor que en las máquinas sincrónicas, la reactancia sincrónica (en % o en por unidad) es dos a tres veces mayor. Con la máquina parada se mide la reactancia de cortocircuito X_cc que corresponde a la reactancia subtransitoria X’’_d y es igualmente del mismo orden de magnitud que ella. Claro no hay arrollamiento inductor no hay ningún valor correspondiente a la reactancia transitoria.

Si bien la constante de ineercia no tiene nada que ver con las reactancias, nos ocuparemos brevemente, ya que ella juega igualmente un papel importante para la magnitud de la máquina y las consideraciones que motivan la elección de cierto valor están estrechamente ligadas a las que motivan también las reactancias.

Cuando se indica en kgm² o en tm² el momento de inercia o el momento de giro PD² de una máquina esto no significa gran cosa. Se va a intentar como para las reactancias, introducir un valor numérico que sea mas expresivo y permita una mejor comparación. Se trata de la constante de inercia H, que es la relación entre la energía cinética de la parte rotante de la máquina a la velocidad sincrónica y la potencia aparente nominal de la máquina. Ella se expresa por consecuencia en kWs/kVA. Para un PD² dado se tiene la fórmula:

Algunos autores utilizan igualmente un valor numérico análogo, la constante de aceleración T_a donde la definición aún no está bien fijada. Se encuentran en efecto tres definiciones diferentes: La constante de aceleración es el tiempo ficticio necesario para llevar la máquina de reposo a la velocidad sincrónica bajo par constante correspondiente a) a la potencia aparente nominal en bornes b) a la potencia activa nominal en bornes o c) a la potencia activa nominal en el eje. Según la definición utilizada entre T_a y H se tiene la relación:

a) T_a = 2 H b) c)

donde cos j es el factor de potencia nominal y h _n el rendimiento a potencia nominal.

En la literatura electrotécnica se utilizan las definiciones a) y b) mientras que la definición c) es utilizada por los proyectistas y usuarios de turbinas.

9.1 Exigencias que conciernen a la reactancia sincrónica.

Por límite de estabilidad estático o potencia de desconexión de una máquina sincrónica, se entiende la potencia máxima que ella puede todavía suministrar hasta antes del desenganche, cuando la potencia aumenta progresivamente. Ella está dada por la fórmula:

donde:

E: fuerza electromotriz interna correspondiente a la excitación

U: tensión fija de la red

Para alcanzar una potencia de desenganche lo más elevada posible, se deberá entonces prescribir para X_eq y X_d un valor pequeño.

Pero esto tiene menos importancia que otras cosas, pudiendo alcanzarse el mismo resultado con la ayuda de un regulador de tensión capaz de elevar rápidamente E a un valor suficiente, al aproximarse al límite de desenganche. Además el límite de estabilidad dinámica (ver párrafo 9.2.1) interviene generalmente antes.

Las largas líneas de alta tensión o las redes de cables pueden representarse con cargas capacitivas muy importantes.

Es así que una línea aérea de 220 kV de 100 km de longitud absorbe una potencia reactiva capacitiva de 13500 kVAr. Si esto quiere lograrse con una excitación positiva la reactancia sincrónica X_d no debe ser mayor que la reactancia de la carga capacitiva X_c, lo que constituye frecuentemente un límite para la reactancia sincrónica de un alternador, límite que puede entonces ser llevado aún más lejos. En el dominio X_q<X_c<X_d la excitación debe ser aún negativa, pero no es tampoco posible obtener todavía un funcionamiento estable de la máquina en este dominio, con la ayuda de dispositivos suplementarios relativamente simples de los que puede disponer un regulador de tensión normal. La condición X_q<X_c constituye en todos los casos un límite que no puede prácticamente ser superado por máquinas de construcción normal.

Frente a perturbaciones rápidas, el flujo en la rueda polar es mantenido, como nosotros ya hemos dicho por la corriente de inducido en su arrollamiento de excitación. La fuerza electromotriz E’ que sigue a la reactancia transitoria (fig. 8) resulta constante y es entonces la reactancia transitoria X’_d que es determinante para la máquina. Para la potencia de desenganche se tiene:

donde X’ es la suma de X’_d y de las reactancias del transformador y de la línea. La parte de estas últimas es generalmente mayor que en el caso de estabilidad estática, porque generalmente la perturbación cuyo efecto debe ser estudiado proviene precisamente del hecho que una parte de las líneas es suprimida a continuación del cortocircuito o de una puesta a tierra accidental. Cuando la estabilidad dinámica es crítica es decir sobre todo cuando la potencia de una central generadora es transportada a gran distancia por una pequeño número de líneas, puede ser útil mantener la reactancia transitoria en un valor tan pequeño como sea posible.

Las estadísticas que conciernen a las grandes redes indican que en las redes de altas y medianas tensiones, las puestas a tierra accidentales y los cortocircuitos bipolares son los accidentes más frecuentes, mientras que los cortocircuitos tripolares son más raros.

En consecuencia la reactancia transitoria debe ser elegida en todos los casos de tal manera que la estabilidad dinámica se mantenga en caso de accidente del primer tipo, con desenganche ultrarrápido y reenganche unipolar de las líneas afectadas. Debe notarse que en caso de accidentes de este tipo un buen amortiguador de jaula contribuye a aumentar muy sensiblemente la estabilidad, cuando el par que el ejerce reduce considerablemente las oscilaciones de la rueda polar durante la perturbación. Este par es en todo un hecho análogo al de un motor asincrónico ordinario, es decir que provoca el frenado cuando la velocidad del alternador pasa la de sincronismo y su aceleración cuando la velocidad es inferior.

Como ya explicamos en el párrafo 3.5 (fig. 8), la reactancia transitoria es igualmente determinante para la variación de tensión debida a una variación de la carga. En el primer instante, la variación de tensión es naturalmente determinada por las reactancias subtransitorias. El pasaje al estado donde la reactancia transitoria es determinante es siempre tan rápido (fig. 16) que aún un el regulador de acción rápida no tiene tiempo de actuar.

En cambio este regulador puede impedir una bajada ulterior de la tensión (fig. 9). El caso de una disminución breve de tensión debajo de cierto límite debe ser evitado, a fin de considerar las exigencias de algunos consumidores (motores a desenganche por tensión nula, instalaciones de iluminación), se está entonces obligado a reducir en consecuencia la reactancia transitoria del alternador.

En un cortocircuito bipolar de un alternador la tercera fase es la sede de una sobretensión. Si esta tercera fase está abierta, la sobretensión máxima alcanza veces la tensión normal de fase. Esta tensión es además afectada por fuertes armónicas, sobre todo la 3ª, 5ª, 7ª y 9ª orden que son más destacadas cuando la relación X’’_q/X’’_d difiere más netamente de 1. Si la tercera fase esta cargada capacitivamente por cables o líneas en vacío la tensión puede ser sensiblemente incrementada por resonancia. A fin de evitar tales sobretensiones es importante que la relación X’’_q/X’’_d no se aparte demasiado de 1 sobre todo en caso de alternadores que deben soportar normalmente importantes cargas capacitivas.

Por esto los arrollamientos amortiguadores completos (X’’_q/X’’_d £ 1,3) y de polos macizos (X’’_q/X’’_d » 1,5) son siempre suficientes. En cambio las jaulas polares son de hecho ineficaces desde este punto de vista (X’’_q/X’’_d = 2 .. 3).

Salvo para las corrientes de cortocircuito instantáneas y las cargas inversas, el valor absoluto de las reactancia subtransitorias juega un papel menos importante que el par ejercido por el amortiguador. Cuando la velocidad de rotación de una máquina sincrónica se aparta de la velocidad de sincronismo, el campo rotante induce en el amortiguador o en el hierro macizo las corrientes que producen un par que tiene carácter idéntico al de un motor asincrónico, como indica la curva típica de la fig. 22 (Variación del par asincrónico del amortiguador en función de la velocidad de rotación La recta punteada indica el par para pequeños desplazamientos en función de la velocidad de rotación sincrónica). A velocidades inferiores que la de sincronismo, el par es motriz, es decir que acelera la rueda polar, mientras que a velocidades que superan la de sincronismo el par es generador, es decir que frena la rueda polar. Para los apartamientos suficientemente pequeños de la velocidad de sincronismo (deslizamiento pequeño), el par es aproximadamente proporcional al resbalamiento:

donde:

P_sn: potencia aparente nominal

n_s: velocidad de sincronismo

n: velocidad instantánea.

El factor de proporcionalidad C_a es llamado constante de amortiguamiento. Ella puede servir de medida de la eficacia del amortiguador. Para la amortiguación de pequeñas oscilaciones, bajo influencia de aquellas la rueda polar sólo se desplaza ligeramente alrededor de una posición determinada y tiene lugar distinguir entre el amortiguamiento por el campo longitudinal C_ad y el amortiguamiento por el campo transversal C_aq que pueden ser muy distintos, sobre todo en el caso de máquinas con jaulas polares. Según las exigencias se obtienen los resultados deseados con polos macizos (C_a = 5..15) con jaulas polares (C_a = 5..25) a menos que sea necesario prever un amortiguador completo (C_a ³ 20). Estos diferentes casos deben ser estudiados en detalle B 14.

Para que una máquina sea capaz de soportar una importante carga inversa, se hace que la reactancia inversa X₂ sea pequeña, y que la sección de cobre eficaz sea grande a fin de tener en cuenta las repercusiones sobre la red, y que la sección de cobre eficaz sea grande, a fin de tener en cuenta el calentamiento. Estas dos exigencias no pueden ser satisfechas más que por un amortiguador completo.

El arranque de motores sincrónicos pone dos exigencias contradictorias; por una parte, se hace un par de arranque tan potente como posible con una absorción de corriente razonable, esto exige un amortiguador de resistencia muy elevada, es decir de pequeña sección. Desde este punto de vista, los polos macizos son muy favorables.

Por otra parte, es necesario que el motor sea igualmente capaz de alcanzar su velocidad de sincronismo a pesar de un par antagónico elevado, esto es aún más difícil cuando el momento de inercia de la máquina a impulsar es considerable. Por ello, es necesario que C_a sea tan grande como posible, es decir se debe prever un amortiguador completo, con una gran sección de cobre. Se deberá entonces decidir por una u otra ejecución, teniendo en cuenta aquellas exigencias que son primordiales En casos muy raros, donde las exigencias son muy elevadas para el arranque y para el desenganche se puede recurrir a una arrollamiento de doble jaula.

Para los alternadores impulsados por una turbina hidráulica, la constante de inercia es prescrita teniendo en cuenta la regulación de la turbina [B 15]. Pero se debe igualmente considerar la estabilidad dinámica y el precio equivalente de la máquina, de manera de no aumentar esta constante más allá de lo estrictamente necesario.

Para los alternadores impulsados por un motor Diesel un aumento de la constante de inercia es frecuentemente necesario, en relación al coeficiente de irregularidad. En numerosos casos, se puede todavía reconocer que la máquina posee un amortiguador suficientemente potente (C_a = 30 .. 40).

Para los motores de compresores a pistones un incremento de H es generalmente inevitable. Más precisamente en este caso, se debe absolutamente evitar ir demasiado lejos, ya que esto hace más difícil el enganche. Para todas las otras máquinas la constante de inercia no debe responder a exigencias especiales.

Cuando las características usuales de una máquina sincrónica son conocidas (potencia aparente, factor de potencia, velocidad de rotación, tensión, frecuencia) y se tienen igualmente en cuenta las prescripciones generales (calentamiento, variación de tensión entre marcha en vacío y plena carga, corriente máxima de cortocircuito instantáneo), se puede establecer un proyecto en el cual las diferentes reactancias y la constante de inercia tengan valores bien determinados.

Estos valores pueden aún ser ligeramente modificados, dentro de ciertos límites sin influir sensiblemente la magnitud del precio de la máquina. Se actúa sobre valores naturales de reactancias y de la constante de inercia.

Para las reactancias más importantes X_d y X’_d la Comisión de estudios de alternadores del CIGRE propone los valores siguientes [B 16]

Los valores naturales de H no están todavía fijados. En el caso de turboalternadores, la turbina de vapor contribuye en buena parte a la constante de inercia de manera que el valor total es relativamente elevado (5..7 kWs/KVA). Para los alternadores impulsados por turbinas hidráulicas, H va de 1 kWs/KVA (pequeñas máquinas rápidas) a 3 kWs/KVA (grandes máquinas lentas). En muy numerosos casos es todavía necesario aumentar estos valores, a fin de tener en cuenta la regulación de la turbina.

Cuando algunas exigencias requieren reactancias más pequeñas, o una constantes de inercia más grande que los valores naturales, las dimensiones de la máquina deben ser igualmente aumentadas, esto conduce naturalmente a un peso y un precio más elevado. Así por ejemplo, una reducción de la reactancia sincrónica X_d a la mitad de su valor natural y una reducción de la reactancia transitoria X’_d a 0,6 a 0,7 veces el valor natural aumenta el precio de la máquina en 20 a 30 % [B 17; 11 y 18; 19].

En la literatura americana, se encuentran numerosas tablas de valores de constantes de máquinas construidas (ver por ejemplo B 18, 19]. En lo que concierne a las máquinas suizas, nosotros hicimos una pequeña tabla de este tipo. Por otra parte reseñas son siempre realizadas en las publicaciones. Algunos ejemplos ligados a máquinas fabricadas por Oerlikon figuran en la Tabla 2.

Las referencias 1, 2 y 3 conciernen a máquinas impulsadas por grandes turbinas de baja velocidad. La máquina 1 representa valores naturales, ella no ha sufrido exigencias limitadoras. Para las máquinas 2 y 3, se han prescrito un momento de inercia fuertemente incrementado y además para la máquina 3 una muy pequeña reactancia sincrónica (en razón de la carga capacitiva debida a las largas líneas de alta tensión).

Las referencias 4, 5, 6 (alternadores de 12 polos) muestran la influencia de distintos tipos de amortiguadores a saber, jaulas polares 4, polos macizos 5, amortiguador completo 6. Esta influencia aparece netamente en los valores de X’’_q que son muy distintos, mientras que los de X’’_d son prácticamente idénticos.

Las referencias 7 y 8 indican los límites entre los cuales varían los alternadores impulsados por motor Diesel.

La referencia 9 corresponde a un compensador mientras que 10 a 12 dan las constantes de algunos motores sincrónicos que caracterizan bien las máquinas modernas de este tipo.

Todas las reactancias indicadas en la tabla son valores no saturados. La máquina Nº 5 tiene polos macizos. Las máquinas Nº^s 4 y 7 tienen grillas polares las demás máquinas una jaula amortiguadora completa.