CÁLCULO DE LÍNEAS Y REDES DE DISTRIBUCIÓN
I
PARÁMETROS Y CARACTERÍSTICAS DE LOS ELEMENTOS DE LOS CIRCUITOS EQUIVALENTES DE LAS REDES ELÉCTRICAS
Los parámetros específicos de las líneas aéreas o de los cables subterraneos, se pueden hallar en las tablas de características técnicas, o bien pueden ser calculados.
La resistencia unitaria o resistencia específica ro se mide en
W/km, y se puede calcular con la siguiente expresión:![]()
donde F es la sección del conductor en mm2,
r es la resistividad medida en W.mm2/km y s es la conductividad medida en m/W.mm2.El valor de la resistividad se expresa generalmente para una temperatura To de 20 ºC. La resistividad para otros valores de temperatura se calcula con la siguiente formula:
![]()
donde
ro es la resistividad a la temperatura To = 20 ºC. y a es el coeficiente de corrección por temperatura, siendo|
Material |
Resistividad r0 Wmm2/km a 20 ºC |
Coeficiente de corrección por temperatura a 1/ºC |
|
Cobre |
17,54 |
0,0039 |
|
Aluminio |
29,5 |
0,0040 |
|
Aleación de Aluminio |
33,3 |
0,0036 |
Para comprender la importancia del incremento de la resistencia eléctrica que ocasiona la temperatura, basta observar que un alambre de cobre de 1 km de longitud y de 1 mm2 de sección que a 20 ºC presenta una resistencia de 1,6
W, a 90 ºC , que es la temperatura admisible en la mayoría de los cables de energía, presentará una resistencia de 22,4 W. Esto es importante a la hora de determinar la caida de tensión y las pérdidas por efecto Joule en una instalación, puesto que, a plena carga, éstos valores llegarían a ser un 27% mayores, que en el caso de considerar la resistividad dada en los textos para corriente contínua y 20 ºC.Los conductores aéreos en régimen normal pueden llegar a alcanzar la temperatura de 80 ºC. Temperaturas mayores que éstas pueden llegar a afectarlo mecánicamente, produciendo su rotura. En régimen de corto circuito, estas temperaturas, pueden llegar a duplicarse, dado que debido a la limitada duración de éstos estados, el cable no llega a ser afectado mecánicamente. Para los cables aislados la temperatura de régimen puede alcanzar los 90 ºC para cable seco y 85 ºC para cable en papel aceite.
Cuando un cable aislado trabaja a temperaturas por encima de las normales, su vida útil se reduce sustancialmente. Se estima que por cada diez grados de exceso sobre la temperatura máxima admisible en servicio permanente, la vida útil de un cable se reduce a la mitad. Esto es, un cable trabajando permanentemente 30 ºC por encima de su temperatura máxima de servicio, reduce su vida útil a poco mas del 10 % de la prevista por el fabricante.
La distribución uniforme de la densidad de corriente en la sección de un conductor, solamente se presenta en corriente contínua. En corriente alterna, a medida que aumenta la frecuencia, la densidad de corriente varía en las distintas zonas de una sección transversal del conductor. Éste fenómeno, que se conoce con el nombre de efecto pelicular, hace que la densidad de corriente aumente desde el interior hacia el exterior del conductor. Éste hecho produce un aumento de la resistencia y una disminución de la reactancia interna del conductor. La distribución de la densidad de corriente en la sección de un conductor, también resulta afectada por los campos magnéticos debidos a la presencia de otros conductores vecinos. Éste fenómeno se conoce con el nombre de efecto de proximidad.
El efecto pelicular, para frecuencias de 50 Hz es despreciable en los conductores de bajas secciones, sin embargo, para secciones grandes de conductores, el efecto pelicular se hace apreciable.
La resistencia unitaria en corriente alterna, a la temperatura T del conductor, se puede calcular por la siguiente formula:
![]()
donde: Ys es el incremento de la resistencia debido al efecto pelicular, e Yp es el debido al efecto de proximidad, siendo de manera suficientemente aproximada:
![]()
siendo: f la frecuencia en Hz, F la sección efectiva en mm2, y
rT la resistividad del conductor a la temperatura T, e:![]()
donde a es la relación entre el diámetro del conductor y la distancia media geométrica entre los ejes de los conductores próximos.
Las dos formulas precedentes son aplicables a cables unipolares; para cables tripolares deberá sustituirse el 3,28 por 5; no deberán utilizarse para conductores de secciones superiores a los 300 mm2.
La reactancia inductiva unitaria o reactancia específica xo por fase de una línea trifásica con conductores de metal no ferroso y transposición de conductores, se calcula por la siguiente formula:
![]()
donde xo se mide en W/km, el logaritmo está tomado en base 10, R es el radio del conductor, Dmed es la distancia media geométrica entre los conductores de la línea, que para una simple terna es:
![]()
Cuando los conductores se disponen en los vértices de un triángulo equilátero de lado D
![]()
si los conductores están dispuestos en forma horizontal:
![]()
donde D es la distancia entre los conductores contiguos.
La suceptancia unitaria o suceptancia específica se mide en 1/W.km y se determina mediante la formula:
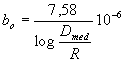
La reactancia inductiva y la suceptancia capacitiva unitarias respectivamente para una línea de conductores en haz son iguales a:
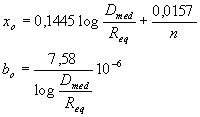
donde n es el número de conductores en la fase, Req el radio equivalente, igual que para un trenzado de fase de dos o tres conductores
![]()
donde amed es la distancia media geométrica entre los conductores de fase.
Una línea aérea de 132 kV puede ser representada mediante un circuito equivalente en forma de cuadripolo P, tal como se muestra en la fig. 1,
en éste circuito se cumplen las siguientes relaciones:
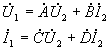
donde:
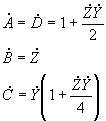
Para el caso de las líneas de media y baja tensión será:
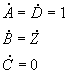
por lo que el circuito equivalente de una línea de media o de baja tensión puede ser representado por una resistencia conectada en serie con una reactancia inductiva, tal como se muestra en la fig 2.
Para verificar que se puede despreciar la suceptancia capacitiva, basta comprobar la potencia reactiva capacitiva que puede tomar la línea con la máxima potencia aparente que se puede transmitir con la misma.
El cálculo de los parámetros de los circuitos equivalentes de los transformadores y autotransformadores supone el conocimiento de los siguientes datos de catálogo:
la relación de transformación kt
las pérdidas en vacio
DPvlas pérdidas de cortocircuito DPcc
la corriente de vacío Iv
Los parámetros de los circuitos equivalentes de los transformadores de doble devanado con potencia nominal Snom se calculan con las formulas
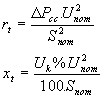
La potencia requerida para el funcionamiento de n transformadores de doble devanado funcionando en paralelo es:

donde ![]() es la carga del transformador.
es la carga del transformador.
Para transformadores de triple devanado con arrollamientos de potencias iguales
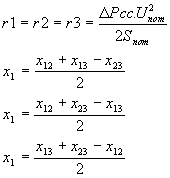
además

Las reactancias inductivas de los autotransformadores se calculan por las mismas formulas que para los transformadores de triple devanado. En éste caso las tensiones de cortocircuito U’cc(1-3)% y U’cc(2-3)% deben ser previamente reducidas a la potencia nominal del autotransformador, si en las tablas de consulta sus valores se indican referidos a la potencia del devanado de baja tensión Sb. Se calculan por medio de las formulas:
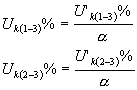
donde a = Sb/Snom.
Para determinar las resistencias del circuito equivalente del autotransformador se utilizan los valores de las pérdidas de cortocircuito, referidas a la potencia nominal del transformador.
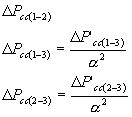
(DP’cc son las pérdidas de potencia referidas a la potencia del devanado de baja tensión). Por éstos datos se hallan:
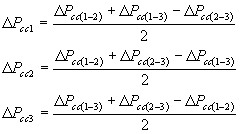
y después se calculan las resistencias del circuito equivalente:
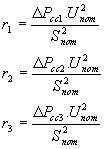
Las pérdidas de potencia en los autotransformadores de triple devanado, para los cuales en las tablas de consulta se indican las pérdidas de cortocircuito DPcc(1-2),
D
Pcc(1-3) y DPcc(2-3), se determinan por medio de las formulas: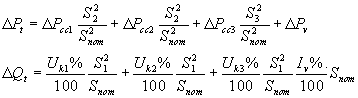
Las pérdidas de energía en todos los elementos de una red eléctrica, conocida la curva de sus cargas, se calcula como:
![]()
y la energía transmitida al consumidor en igual intervalo de tiempo, como:
![]()