![]() APLICACIÓN DE LAS TRANSFORMACIONES LINEALES EN EL CÁLCULO DE LAS REDES ELÉCTRICAS
APLICACIÓN DE LAS TRANSFORMACIONES LINEALES EN EL CÁLCULO DE LAS REDES ELÉCTRICAS
Autor: Ing. Guillermo Loscalzo
Nos proponemos mostrar ciertas propiedades de aplicación al cálculo de redes eléctricas en régimen estable. La utilidad de éste método consiste en que facilita, mediante el empleo de computadoras, diseñar y conocer las condiciones de funcionamiento de los sistemas eléctricos. Los métodos a considerar se refieren al caso en que las cargas están dadas por las corrientes de carga, determinadas a partir de las potencias de carga, las cuales por lo general son conocidas. El estado de régimen de la red determina la distribución de las corrientes, las cuales se determinan a partir de los parámetros conocidos del circuito de la red y de las corrientes de carga.
Utilizando como herramienta el método matricial expondremos ciertas propiedades de las redes que nos permitirán determinar la distribución de la corriente en cada una de las ramas de los circuitos, por lo que se deberá también escribir en forma matricial, el conjunto de corrientes, tensiones, parámetros de red y los vínculos entre ellos, correspondientes a la configuración de la red. Las relaciones entre todas ésta matrices se establecen en base a las leyes de Kirchhoff. Después de hallar la distribución de las corrientes, las tensiones en los nodos y las caídas de tensión en las ramas, se determinará el flujo de carga y las pérdidas de potencia en las ramas.
1.-
ALGUNAS DEFINICIONES SOBRE LAS REDES ELÉCTRICASRÉGIMEN: es el estado del sistema que se caracteriza por índices que cuantitativamente definen su funcionamiento. Éstos índices se denominan parámetros de régimen; a los mismos pertenecen los valores de la potencia, tensión, corriente, ángulos de desplazamiento de los fasores de f.e.m. tensiones, corrientes etc. Los parámetros de régimen están vinculados por correlaciones en los cuales se incluyen los parámetros del sistema.
Los parámetros del sistema son los índices que cuantitativamente determinan las propiedades físicas del sistema. A éstos parámetros pertenecen por ejemplo los valores de las impedancias y las relaciones de transformación de los transformadores.
Consideremos ahora una red eléctrica como la indicada en la
fig. 1, conformada por cinco ramas , donde cada una de las ramas se designa por los números 1, 2, 3, 4, y 5; y sean sus impedancias Z1 , Z2 , Z3 ,Z4 , Z5 , respectivamente en cuyos nodos a, b y c se tienen las corrientes de carga Ja , J b , Jc y sea el nodo A el correspondiente al punto de suministro de energía.Llamaremos ÁRBOL de una red a aquella parte de la misma compuesta por un número suficiente de ramas para poder conectar todos los nudos sin formar un paso cerrado. En la
fig. 1 el ARBOL se puede considerar formado por las ramas 1, 2 y 3.Llamaremos RAMAS DE UN ÁRBOL a cada una de las ramas que conforman el ÁRBOL. En la
fig. 2 se representa el ÁRBOL de la red.Aquellas ramas de la red que no forman parte de un árbol las llamaremos UNIONES (LINKS). En la
fig. 1 las UNIONES estarían conformadas por las ramas 4 y 5.2.- LA MATRIZ DE CONEXIÓN NODAL
Podemos representar la red de la
fig. 1 sin dibujar las impedancias tal como se muestra en la fig. 3, asignando sobre cada rama un sentido positivo presunto para las corrientes y para cada una de las mallas independientes elegidas un sentido de recorrido, que en nuestro caso lo designamos con los números romanos I y II. El sentido de recorrido de las dos mallas se ha tomado en sentido antihorario. Por cada una de las ramas circularan las corrientes I1 , I2 , I3 , I4 y I5 , y las tensiones en cada una de las ramas serán: I1Z1 , I2Z2 , I3Z3 , I4Z4 , y I5Z5 .Mediante la aplicación de la primera ley de Kirchhoff se pueden establecer las relaciones entre las corrientes de rama y las corrientes de carga. La red dada en nuestro caso tiene cuatro nudos, por lo que el número de ecuaciones independientes será 4 – 1 = 3
![]()
![]()
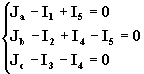 (1)
(1)
Al nodo A que no se incluye en el sistema de ecuaciones (1) se lo llama NODO DE REFERENCIA y en nuestro caso coincide con el punto de suministro.
Las ecuaciones (1) se pueden escribir:
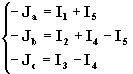 (2)
(2)
Éste sistema lineal de ecuaciones puede ser escrito en forma matricial de la siguiente manera:
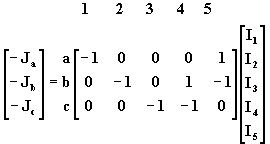 (3)
(3)
y en forma resumida se puede escribir:
J
= N I (4)donde N es la matriz de los coeficientes de las corrientes de rama. Los números escritos en la parte superior de la matriz N en la expresión (17) indican la rama a que corresponde cada cuadricula de la matriz y las letras escritas a la izquierda de la misma indican el nudo correspondiente a cada cuadrícula de la matriz. La matriz N se llama MATRIZ DE CONEXIÓN NODAL. . I es la matriz columna de las corrientes de rama. La matriz
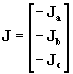 (5)
(5)
es la matriz de las corrientes de carga, la cual queda definida de ahora en mas como la matriz de las corrientes de carga.
La matriz N se puede calcular en forma práctica, teniendo en cuenta que cada cuadrícula puede tomar el valor +1, -1 o 0. Es posible establecer una correlación entre cada corriente de rama y cada nudo de la red con cada cuadrícula de la matriz N. Cuando la corriente de rama sale del nudo considerado el coeficiente será +1, si la corriente de rama entra al nudo el coeficiente será –1, y si la corriente de rama no converge al nudo considerado el coeficiente es 0.
La matriz N se puede subdividir en dos submatrices: la submatriz Na donde sus columnas corresponden a las ramas del árbol y la submatriz Nu donde sus columnas corresponden a las ramas de las uniones.
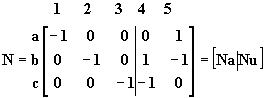 (6)
(6)
3 - LA MATRIZ DE CONEXIÓN DE MALLAS
Apliquemos ahora a la red de la fig. 3 la segunda ley de Kirchhoff: para la malla I:
![]() (7)
(7)
para la malla II:
![]() (8)
(8)
podemos expresar las ecuaciones (7) y (8) en forma matricial:
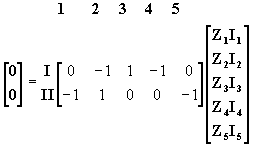 (9)
(9)
que en forma resumida se puede escribir:
0 = M ZI (10)
donde M es la matriz de los coeficientes de las tensiones en las impedancias de cada rama. Los números escritos en la parte superior de la matriz M indican la rama a que corresponde cada cuadrícula de la matriz y los números romanos escritos a la izquierda de la matriz indican la malla a la cual corresponde cada cuadrícula de la misma. La matriz M se llama MATRIZ DE CONEXIÓN DE MALLAS.
La matriz M puede ser calculada en forma práctica teniendo en cuenta que cada cuadrícula puede tomar el valor +1, -1 o 0. Cuando el sentido de recorrido de la malla coincide con el sentido positivo asignado presunto a cada corriente de rama, el coeficiente será +1, si la corriente de rama tiene un sentido positivo asignado presunto contrario al sentido de recorrido de la malla, el coeficiente es –1. Cuando la rama considerada 3n la matriz no pertenece a la malla recorrida, el coeficiente correspondiente será 0. También en éste caso la matriz M se puede subdividir en dos submatrices: la submatriz Ma cuyas columnas corresponden a las ramas del árbol y la matriz Mu cuyas columnas corresponden a las ramas de las uniones.
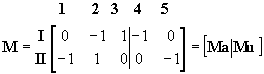 (11)
(11)
4.-LA TRANSFORMACIÓN DE LAS CORRIENTES DE MALLA EN CORRIENTES DE RAMA
Consideremos el circuito de la fig. 4 , similar al correspondiente al de la fig. 3, pero con la diferencia de que en ésta oportunidad se han conectado a las ramas 1, 2 y 3 las fuentes de f.e.m. E1, E2 y E3 respectivamente. Fijado el sentido de recorrido para las mallas independientes I y II, llamamos II e III a cada una de las corrientes de malla correspondientes a las mismas. Como ya se ha mencionado, el arbol de la red está formado por las ramas 1, 2 y 3, en donde consideraremos ahora que la rama 1 tiene en común la corriente de malla II y la corriente de carga Ja , considerada ésta última como una corriente de malla común a la rama 1. La rama 2 tiene en común las corrientes de malla II , III y la corriente de carga Jb considerada ésta como corriente de malla colindante con la rama 2. Finalmente la rama 3 tendrá en común las corrientes III e Jc. Es decir que se han tomado las corrientes de carga como corrientes de malla comunes a cada una de las ramas que conforman el árbol de la red, o se que si llamamos I1 , I2 , I3 , I4 e I5 a las corrientes de rama, se cumplirá que:
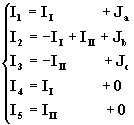 (12)
(12)
Podemos llevar ésta última expresión a la forma matricial, para ello recordemos que precedentemente se ha definido a J mediante la formula matricial (5).
Si consideramos éstas corrientes como pertenecientes a las ramas del árbol en ausencia de las uniones tal como se muestra en la fig. 5 podemos escribir:
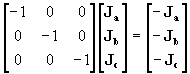 (13)
(13)
donde Ja , Jb , Jc ,corresponden a las corrientes que circulan por el árbol cuando no están conectadas las uniones (ramas 4 y 5), es decir que la matriz de las corrientes de rama de la fig. 5 será igual a la matriz de las corrientes de carga cambiada de signo. La matriz dada en la expresión (13)
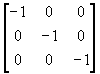 (14)
(14)
corresponde a la matriz nodal del árbol Na. Corrientes de rama sin conectar las uniones serán entonces
![]() (15)
(15)
donde Na-1 es la matriz inversa de la matriz de conexión nodal,.de Na, la cual es posible calcular ya que se trata de una matriz cuadrada y J es la matriz de las corrientes de carga en forma desarrollada será
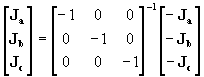 (16)
(16)
podemos ahora proponernos escribir el sistema de ecuaciones (12) en forma matricial:
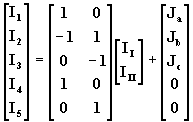 (17)
(17)
donde la matriz de la derecha, teniendo en cuenta la (15) se puede representar como una matriz compuesta de la siguiente manera:
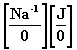 (18)
(18)
la matriz de los coeficientes de II e III que aparece en la (17):
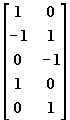 (19)
(19)
es la matriz transpuesta de la matriz de conexión de mallas y la llamaremos Mt , por lo que la expresión (17) se puede escribir:
 (20)
(20)
donde Ir es la matriz de las corrientes de rama, Mt la matriz transpuesta de la matriz de conexión de mallas IM la matriz de las corrientes de malla y 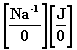 representa la incidencia de las corrientes de carga en las corrientes de rama.
representa la incidencia de las corrientes de carga en las corrientes de rama.
5.- LA TRANSFORMACIÓN DE LAS f.e.m. DE RAMA EN f.e.m. DE MALLA
Continuando con el análisis del circuito de la fig. 4, observamos que la matriz de conexión de mallas será la misma que la dada en la expresión (9) :
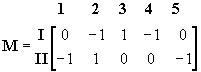 (21)
(21)
Apliquemos ahora a la red de la fig. 4 la segunda ley de Kirchhoff:
 (22)
(22)
Los primeros miembros de éste sistema de ecuaciones se puede obtener multiplicando la matriz de conexión de mallas M por la matriz columna formada por las f.e.m. conectada a cada una de las ramas de la red, que llamaremos Er. En efecto:
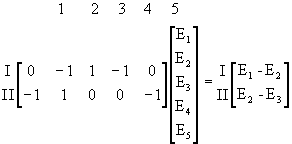 (23)
(23)
y en forma resumida:
![]() (25)
(25)
siendo EM la matriz columna de las f.e.m. de malla.
6.- LA TRANSFORMACIÓN DE LAS CAIDAS DE TENSIÓN EN LOS NODOS EN LAS CAIDAS DE TENSIÓN EN LAS RAMAS DE LA RED
Continuando el análisis de la red de la fig. 4, y adoptando como nodo de referencia el nodo A, el potencial en los nudos a, b y c estará dado por la siguiente matriz:
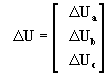 (26)
(26)
siendo DUa = Ua – UA , DUa = Ub – UA , DUa = Uc – UA .Las caídas de tensión en cada una de las ramas de la red se puede expresar:
 (27)
(27)
la (26) y la (27) se pueden relacionar mediante la matriz de transformación nodal transpuesta formulada en la expresión (3):
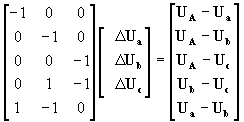 (28)
(28)
la matriz de la izquierda es la matriz transpuesta de la matriz de conexión nodal, que llamaremos Nt , por lo que en forma resumida podremos escribir
![]()
![]() (29)
(29)
7.- LA TRANSFORMACIÓN DE LAS IMPEDANCIAS DE RAMA EN LAS IMPEDANCIAS DE MALLA
Teniendo en cuenta las ecuaciones (17), (20), (23), y (25) sistema de ecuaciones (22) se puede escribir matricialmente de la siguiente manera:
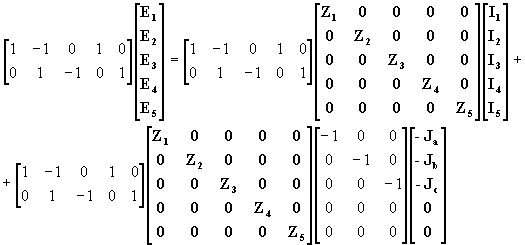 (30)
(30)
la cual se puede escribir también de la siguiente manera:
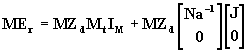 (31)
(31)
donde M representa la matriz de conexión de mallas Er la matriz de las f.e.m conectadas a cada una de las ramas de la red, Zd la matriz diagonal de las impedancias de rama, Mt representa la matriz transpuesta de la matriz de conexión de mallas, IM la matriz de las corrientes de las mallas determinadas por las ramas de la red, mientras que el término 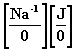 como ya fue analizado a partir de la ecuación (20), representa la incidencia de las corrientes de carga en las corrientes de rama.
como ya fue analizado a partir de la ecuación (20), representa la incidencia de las corrientes de carga en las corrientes de rama.
La expresión (31) nos permite observar la forma en que se transforma la matriz de impedancias Zd cuando se consideran las corrientes de malla, en lugar de las corrientes de rama, a ésta impedancia la llamaremos matriz de impedancias de mallas ZM, la cual se puede obtener también mediante la aplicación del teorema de las corrientes de malla; en ésta matriz de impedancias los elementos no pertenecientes a la diagonal principal no serán todos iguales a cero. La ley de transformación que permite pasar de la matriz de impedancias de rama a la matriz de impedancias de malla estará dada entonces por la siguiente expresión:
![]() (32)
(32)
En cuanto a la ley de transformación de Zd cuando incide sobre las corrientes de carga se podrá expresar:
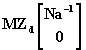 (33)
(33)
En el caso de que se trate de una red como la de la fig. 3 en donde el nodo A es el punto de suministro de corriente y en donde en las ramas 1, 2, 3, 4 y 5 de la red no se encuentran conectadas fuentes de f.e.m. , la ecuación (31) adopta la siguiente forma:
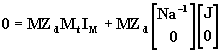 (34)
(34)
8.- LA TRANSFORMACIÓN DE LAS IMPEDANCIAS DE RAMA EN LAS IMPEDANCIAS DE NODO
Consideremos la red de la fig. 4 y escribamos la ley de Ohm para cada una de las ramas de la red
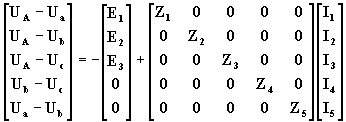 (35)
(35)
o bien:
![]() (36)
(36)
donde Ur es la matriz de tensiones entre los extremos de cada rama, Er la f.e.m. conectada en cada rama, Zd la matriz diagonal de las impedancias de rama e Ir la matriz de las corrientes de rama. Teniendo en cuenta la (29) la (36) se puede escribir:
![]()
![]() (37)
(37)
multiplicando la (37) por Z-1 resulta:
![]()
![]() (38)
(38)
![]() (39)
(39)
teniendo en cuenta la (3) y la (4) podemos escribir la matriz de las corrientes de rama en función de las corrientes de carga, para ello bastará multiplicar la (39) por la matriz de conexión de nudos N:
![]() (40)
(40)
![]() (41)
(41)
de la (41) podemos despejar DU, de donde resulta que:
![]()
![]() (42)
(42)
donde ![]() se llama matriz de impedancias nodales y la designaremos con la notación ZN . La ley de transformación que permite pasar de la matriz de impedancias de rama a la matriz de las impedancias de nodo resulta entonces ser:
se llama matriz de impedancias nodales y la designaremos con la notación ZN . La ley de transformación que permite pasar de la matriz de impedancias de rama a la matriz de las impedancias de nodo resulta entonces ser:
![]() (43)
(43)
el término![]() se puede determinar como la matriz de admitancias mediante la aplicación del teorema e los potenciales de nodo y la designamos con la notación YN.
se puede determinar como la matriz de admitancias mediante la aplicación del teorema e los potenciales de nodo y la designamos con la notación YN.
En el caso en que no se tengan fuentes de f.e.m. conectadas a las ramas de la red en estudio, como pasa en el caso de la fig. 3 en que el circuito se alimenta desde el nodo A, la (42) se podrá escribir de la siguiente manera:
![]() (44)
(44)
Si al nodo A le asignamos el potencial UA , la tensión en cada nodo será:
![]() (45)
(45)
En ausencia de fuentes de f.e.m. en las ramas de la red en estudio, las corrientes en cada una de las ramas se puede calcular con la siguiente expresión:
![]() (46)
(46)
donde Yd es la matriz diagonal de admitancia de las ramas de la red.
9.- MATRIZ DE LA POTENCIA TOTAL EN LAS RAMAS DE UNA RED ALIMENTADA DESDE UNO DE SUS NODOS
Consideremos la red de la fig. 3 y escribamos la expresión de las potencias en forma matricial, con la convención de asignar signo positivo a las potencias que salen de un nudo y signo negativo a las potencias que entran al nudo:
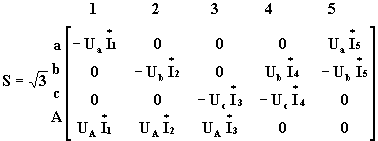 (47)
(47)
siendo Ua, Ub y Uc las tensiones en los nudos a, b y c.
![]() son las potencias suministradas en el nodo A a las ramas 1, 2 y 3.
son las potencias suministradas en el nodo A a las ramas 1, 2 y 3.
![]() es la potencia suministrada por la rama 1 en el nodo a ,
es la potencia suministrada por la rama 1 en el nodo a ,
![]() es la potencia suministrada por la rama 2 en el punto b,
es la potencia suministrada por la rama 2 en el punto b,
![]() es la potencia suministrada por la rama 3 en el punto c.
es la potencia suministrada por la rama 3 en el punto c.
Sumando los elementos de la columna 1 se obtienen las pérdidas de potencia de la rama 1 = DS1
Sumando los elementos de la columna 2 se obtienen las pérdidas de potencia de la rama 2 = DS2
Sumando los elementos de la columna 3 se obtienen las pérdidas de potencia de la rama 3 = DS3
Sumando los elementos de la columna 4 se obtienen las pérdidas de potencia de la rama 4 = DS4
Sumando los elementos de la columna 5 se obtienen las pérdidas de potencia de la rama 5 = DS5
La perdida de potencia en las ramas de la red es:
![]()
![]() (48)
(48)
Este valor obtenido deberá ser el mismo que la diferencia entre la potencia suministrada en A SA y la potencia de las cargas Sa , Sb ,y Sc o sea:
![]() (49)
(49)
La matriz (47) se puede obtener como el producto de dos matrices:
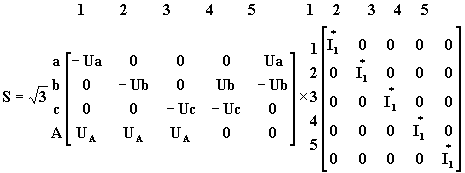 (50)
(50)
La matriz de las tensiones precedente se puede obtener multiplicando la matriz diagonal de tensiones de nodo de orden 4x4 por la matriz de conexión nodal en la que se incluye además de los nodos a, b y c, el nodo A, o sea:
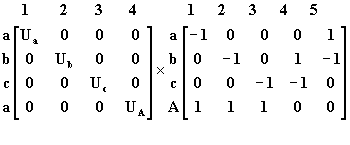 (51)
(51)
Llamando Und a la matriz diagonal de las tensiones de nodo, la (51) se puede escribir:
![]() (52)
(52)
donde NS es la matriz de conexión nodal incluido el nodo A. Finalmente la (50) se puede obtener mediante el siguiente producto de tres matrices:
![]() (53)
(53)
siendo Id la matriz diagonal de las corrientes de rama.
10.- APLICACIÓN: METODOS DE RESOLUCION ITERATIVOS
Cuando el número de ecuaciones del sistema es muy elevado, como ocurre en muchos problemas de redes eléctricas, resulta de utilidad emplear procedimientos de aproximaciones sucesivas tal como el método iterativo para resolución de sistemas de ecuaciones lineales de Gauss – Seidel.
10-1) DESCRIPCIÓN DEL MÉTODO DE ITERACIÓN. (Para mayor información se puede consultar Calculo Numérico y Gráfico de M. Sadosky – capítulo VI – párrafo 17).
Para simplificar consideraremos un sistema de tres ecuaciones con tres incognitas:
![]()
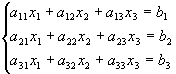 (54)
(54)
cuando los coeficientes del sistema son simétricos o cuando los coeficientes de la diagonal principal son mucho mayores que los restantes se cumplen las condiciones para que el procedimiento sea convergente, y entonces es posible aplicar el método de iteración.. En éstas condiciones, el proceso de iteración se puede iniciar haciendo los coeficientes ![]() para
para ![]()
![]() , resultando así, la siguiente aproximación inicial:
, resultando así, la siguiente aproximación inicial:
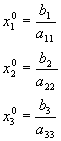 (55)
(55)
reemplazando los valores obtenidos en (55) en la (54) resulta:
 (56)
(56)
teniendo en cuenta las (54) las (55) quedan:
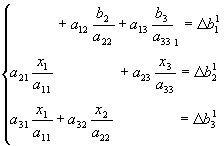 (57)
(57)
la (56) se puede escribir también:
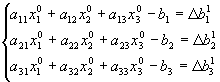 (58)
(58)
suponiendo que las x del sistema (54) representan la solución exacta, restando al sistema (54) el sistema (58) resulta:
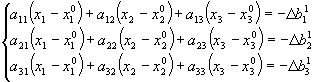 (59)
(59)
la diferencia entre las ![]() siendo (i = 1, 2,3) representa la diferencia entre el valor verdadero y el valor calculado en la primera aproximación, y lo llamaremos
siendo (i = 1, 2,3) representa la diferencia entre el valor verdadero y el valor calculado en la primera aproximación, y lo llamaremos ![]() , o sea que
, o sea que
![]() (60)
(60)
de donde la (59) queda:
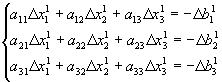 (61)
(61)
En forma matricial el proceso de calculo puede resumirse de la siguiente manera: supongamos que hubiésemos llegado al orden de iteración k, por lo que serán conocidas las ![]() , entonces los
, entonces los ![]() se calculan mediante el siguiente producto de matrices:
se calculan mediante el siguiente producto de matrices:
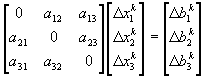 (62)
(62)
los nuevos valores de las ![]() , se obtienen mediante la siguiente operación matricial:
, se obtienen mediante la siguiente operación matricial:
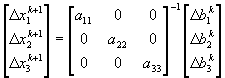 (63)
(63)
La matriz de las incógnitas se determina del siguiente modo:
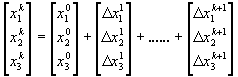 (64)
(64)
10 – 2) APLICACIÓN DEL METODO DE ITERACIÓN UTILIZANDO LAS LEYES DE KIRCHHOFF Y EL TEOREMA DE LAS CORRIENTES DE MALLA
Apliquemos la segunda ley de Kirchhoff al circuito de la fig. 3:
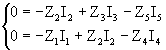
y en forma matricial:
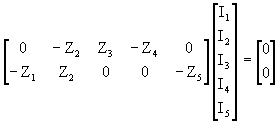 (66)
(66)
llamando a la matriz de impedancias ZK y a la de corrientes de rama Ir, la (66) se puede escribir:
![]() (67)
(67)
En primera aproximación se puede determinar las corrientes de carga dividiendo la potencia por ![]() y por la tensión en el nodo A:
y por la tensión en el nodo A:
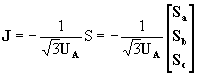 (68)
(68)
donde S representa la matriz columna de las potencias de carga; de este modo se obtiene:
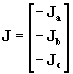 (69)
(69)
Fijamos ahora arbitrariamente el valor de la corriente en tantas ramas del circuito como número de mallas independientes tengamos; en nuestro caso tendremos dos ramas: la I10 y la I20; quedando así definido el resto de los valores de las corrientes pertenecientes a las otras ramas, por aplicación de la primera ley de Kirchhoff:
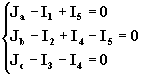 (70)
(70)
naturalmente, éstos valores de corriente no serán los verdaderos, pero con la aplicación del método iterativo, éstos van a converger rápidamente a los valores de corrientes verdaderos.
La matriz de las corrientes arbitrarias de rama será
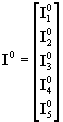 (71)
(71)
reemplazando éstos valores de corriente en la expresión (66), es evidente que ésta última no va a dar cero, sino que resultará una matriz distinta de cero.
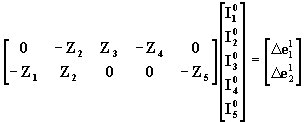 (72)
(72)
o bien
![]() (73)
(73)
ésta última operación se llama de iteración cero. Con el proceso iterativo se busca hacer la matriz
De tan pequeña como se desee.El segundo paso se llama primera iteración. Aplicamos en ésta instancia el teorema de las corrientes de malla que nos va a permitir determinar dos corrientes de malla la DII1 y la DIII1 .
Como se mostró en la (62), aplicando la (34) queda:
![]() (74)
(74)
El proceso iterativo se puede interpretar eléctricamente, observando que por aplicación de las corrientes de malla a determinar se busca producir valores De con signo distinto al obtenido en la operación (72), que irán disminuyendo en valor absoluto y tendiendo a cero en la medida que avance el proceso itrativo. Por ésta razón las DIM se llaman corrientes igualadoras de malla.
Las corrientes igualadoras de rama serán
![]() (75)
(75)
La matriz de las corrientes de rama en la primera iteración será:
![]() (76)
(76)
de la misma manera se sigue el proceso iterativo para la segunda, tercera, etc. Iteración, hasta alcanzar en el cálculo la iteración deseada.
10-3) MÉTODO DE RESOLUCIÓN ITERATIVO CON APLICACIÓN DEL TEOREMA DE LOS POTENCIALES DE NUDO.
Consideremos el circuito de la fig. 3. Tomamos como nodo de referencia el nodo A. La matríz de las tensiones nodales será igual a la tensión en el nodo de referencia menos la caída de tensión dada por la (45)
![]() (77)
(77)
D
U está precedida con signo positivo pues los valores de sus componentes matriciales son negativos.Teniendo en cuenta la (44)
![]() (78)
(78)
donde se supone que Un es el valor de la matriz de tensiones verdaderos en los puntos de conexión de las cargas. Para la iteración cero asignamos a las tensiones componentes de la matriz de tensiones nodales valores arbitrarios
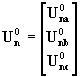 (79)
(79)
de distinto valor que las componentes de la matriz de las tensiones verdaderas. Si reemplazamos la (79) en la (78) resulta:
![]() (80)
(80)
recordando que NZd-1Nt es la matriz de admitancias que también se puede obtiener por aplicación del teorema de los potenciales de nodo y que llamaremos YN resulta:
![]() (81)
(81)
o bien, llamando YN-1= ZN de la (80) se obtiene:
ZN(YNUA+J-YNUn0)=
DUn1 (82)como ya se indicó en la formulas (60) y (64) el nuevo valor de la tensión será:
Un1
= Un0 +DUn1 (83)la (82) se escribirá ahora:
![]()
y así sucesivamente hasta alcanzar el grado de precisión que se desee.
De acuerdo al método de iteración, teniendo en cuenta la (63), la ZNd estará conformada por la matriz diagonal
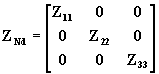
que se obtienen como la inversa de la matriz diagonal de admitancias nodales, suponiendo que todos los elementos de ésta matriz a excepción de los diagonales son iguales a cero:
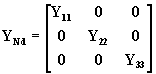
donde YNd-1=ZNd , por lo que para después del paso de iteración k la (84) se puede escribir
![]()
siendo.
![]()