CALCULOS MECANICOS DE LOS CONDUCTORES
I. Introducción
El transporte de la energía eléctrica desde el punto de generación hasta los centros de distribución o consumo se realiza, como ya hemos visto anteriormente, mediante cables aislados subterráneos o mediante conductores aéreos desnudos.
En ambos casos el dimensionamiento de la sección está regido por: corriente a transmitir, caída de tensión, cortocircuito y cálculo mecánico. En el caso de los cables subterráneos el mismo lo realiza el fabricante, en general, y se limita a dar las pautas en cuanto a las tracciones máximas durante el tendido del cables y los radios de curvatura. En cambio la línea aérea debe ser calculada mecánicamente por el proyectista.
El cálculo mecánico consiste en la determinación de las tensiones mecánicas que soportan y las flechas que asumen los conductores de fase y el cable de guardia.
Se calculan las tensiones mecánicas para verificar que en ningún caso, cualquiera sea la carga, se supere el límite de rotura elástica o por fatiga del conductor.
En la práctica y en base a experiencias de líneas existentes, para cada tipo de conductor y región climática, se normalizan las tensiones máximas admisibles en los conductores, para limitar las averías de las líneas eléctricas evitar el sobredimensionamiento del soporte y racionalizar los cálculos.
La flecha se calcula para que ningún caso asuma valores mayores que reduzcan la altura mínima de los conductores sobre el suelo. A igual que las tensiones, las alturas mínimas respecto al suelo se encuentran normalizadas en función de la zona que atraviesa la línea.
A continuación nos ocuparemos de analizar mecánicamente el comportamiento de los conductores para líneas aéreas eléctricas y como encarar los cálculos de las tensiones mecánicas y flechas de los mismos.
II. Cálculo de un cable suspendido entre dos puntos fijos a igual nivel.
Supongamos tener suspendido un cable entre dos puntos fijos con vinculación de articulación libre (ver figura 1).
Al analizar el comportamiento del conductor, podemos limitarnos a tomar elementos infinitésimo (ds) en un punto del conductor y estudiar su comportamiento.
Separando ficticiamente el segmento ds de la cuerda conformada, para mantener el equilibrio debemos sustituir por dos fuerzas como se indica en la figura 1 y figura 2
Como referencia se ha tomado el sistema de coordenadas x e y.
En la figura 2 se pueden observar tres fuerzas, que son F, (F = DF), G. ds. Descomponiendo las mismas según los ejes x e y, tendremos los componente según ambas direcciones, partiendo de la condición de que ser un sistema en equilibrio la sumatoria debe ser nula, dando signo positivo a los vectores que apuntan hacia arriba y hacia la derecha, tendremos:
Proyectando sobre el eje x
de donde resulta que dH = O, único resultado que satisface la igualdad. Luego se deduce que el valor de H es constante a lo largo de la cuerda en estudio.
Proyectando sobre el eje y.
S X = 0 = -V + (V + dV) - G. ds
0 = dV - G. ds
dV = G. ds
Descomponiendo también ds según ambas direcciones, figura 3, tendremos:
![]()
![]()
multiplicando y dividiendo, el segundo término de la igualdad por dx.
![]()
![]()
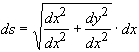
denominando a dy/dx = y, tendremos que:
![]()
luego reemplazando
![]() ‚
‚
pero como
dV = G. ds
podemos reemplazar ‚ en
![]() ƒ
ƒ
Como la derivada en cualquier punto de la cuerda es la tangente y está en el punto que estamos analizando es igual a V/H podemos escribir que:
![]()
luego
![]()
derivando
![]() „
„
Igualando ƒ con „ , tendremos
![]()
reagrupando términos
![]()
denominando a H/G como h, obtendremos
![]()
Para reconocer la ecuación, llamamos
z = y por lo tanto y" = z = dz/dx
remplazando en
![]()
![]()
integrando y resolviendo
![]()
![]()
![]()
cuando X = O C = O por lo tanto
![]()
expresándolo en forma de la función trigométrica, obtendremos.
z = sh (x / h)
recordando que z = y dy / dx
![]()
reagrupando
![]()
Integrando y resolviendo
![]() ECUACION DE CATENARIA
ECUACION DE CATENARIA
la constante C1 será nula cuando x = O
Desarrollando en serie la ecuación hiperbólica, tenemos
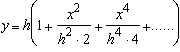
A partir de ésta podemos realizar una serie de hipótesis simplificativas
1) Podemos despreciar el tercer término, que está elevado a la cuarta potencia, siempre que h4 sea mucho mayor que x4, con lo que obtenemos la ecuación de una parábola.
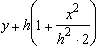
![]()
Con esta sustitución y para vanos menores de 400 m (que es la corriente en línea de transmisión) con flechas menores del 6 % del vano, el error que se comete en la determinación de la flecha es menor del 0,5 % (tal demostración se hará mas adelante).
2) recordando que h = H/G, la fuerza horizontal H es la tensión mecánica del conductor multiplicado por la sección, en N, en el centro del vano. A esta la denominamos Po, que también es posible expresarla como Po = po. S, donde po, es la tensión mecánica específica, en N/mm2, y S la sección del conductor. En realidad en lugar de trabajar con po correspondería usar pi que es mas general, ya que la tensión mecánica a lo largo del conductor en todo el vano es variable. posteriormente se demostrará que p @ pi @ po.
Expresando el peso por unidad de longitud G también en función de la sección, se tiene que G = g.S, en donde g es el peso específico en Kg/m.mm2; por lo tanto:
![]()
No interesa extremar la precisión, pues se hacen una serie de consideraciones que a veces se cumplen y otras no, por ej. si se tiene en cuenta un viento de 120 Km/h, a lo mejor una sola condición. Lo mismo vale para el hielo.
Volviendo a la figura 1, siendo h la distancia al conductor desde la osbscisa resulta que la flecha de la cuerda será:
![]()
![]()
Como hemos demostrado, para cualquier punto.
![]()
Además la flecha será máxima en la mitad del vano a, siempre que las cargas sean uniformes y el terreno horizontal, es decir.
![]()
por lo tanto
![]()
luego
![]()
reemplazando
![]()
![]()
![]()
A partir de estos últimos razonamientos y con la ayuda de la figura 3 probamos la factibilidad de la hipótesis simplificativa 2.
p es la composición de G.L/2
![]()
con el fin de expresar la anterior en función de tensión mecánica y peso especifico, es necesario plantear la hipótesis simplificativa 3:
El largo del conductor 1 es igual al vano a, luego se demostrará que 1 @ a. Teniendo en cuenta lo establecido y analizado la figura 4, surge:
![]()
![]()
![]()
en definitiva
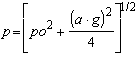
desarrollando la última expresión en Serie
![]()
donde el número combinatorio ![]() vale
vale
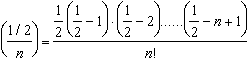
para el caso tratado el último combinatorio es igual al primero, en efecto 1/2 es el primero y (1/2) = 1/2/n! es el último.
![]()
reemplazando
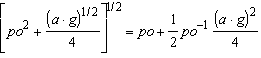
entonces
![]()
recordando que
![]()
por lo tanto
![]() (Po = P, en el centro del vano)
(Po = P, en el centro del vano)
La flecha máxima en los conductores es aproximadamente 5m para vanos del orden de los 200 a 300 m. En el caso de conductores de cobre, de peso específico = 8,9 Kg/dm3 tratando el cobre con una Pr = kg/mm2 y suponiendo padm = 20 Kg/mm2; tenemos:

Suponiendo un conductor de Al/Ac con = 35,4.10-4 kg/m.mm2 y para un vano a = 400m, resulta una flecha de 10m en ese caso, si su tensión fuera de 10 kg/mm2.
![]()
Puede apreciarse que la diferencia entre ![]() es despreciable, utilizándose en consecuencia p ó po indistintamente.
es despreciable, utilizándose en consecuencia p ó po indistintamente.