ing. Alfredo Rifaldi

Las cubas electrolíticas, otros medios analógicos, y la buena mano de artistas gráficos, permitieron a mediados del siglo pasado desarrollar hermosos dibujos que representaban campos eléctricos, magnéticos, flujos de gases, líquidos, campos térmicos, campos de fuerzas, campos de tensiones, etc.

Una idea que tenia fija en mi mente desde hace años, y que me parecía útil para entusiasmar en el estudio de campos, era hacer una colección de las hermosas figuras que los representan y que se observan en distintos libros, revistas, y en muchos casos en hojas de propaganda.

En cierto momento a un compañero de trabajo, excelente dibujante con programas CAD, y a la sazón estudiante de ingeniería, le asignaron como trabajo practico desarrollar un programa que resolviera la ecuación diferencial de Laplace por el método de relajación, y pretendí ayudarlo.

Mi experiencia previa era que hace años había copiado algunos programas que desarrollaban esta tarea y cuyos resultados aparecían impresos con caracteres alfanuméricos esta era una forma de graficar de un pasado que hoy parece remoto.

Rápidamente logramos éxito con el programa, la resolución, cuyos resultados entregamos a otro programa que ya estaba en uso desde hacia mucho tiempo para representar isolux (determinadas por un programa de cálculo de iluminación) o equipotenciales (correspondientes a un programa de cálculo del potencial en la superficie del terreno debido a una red dispersora que inyecta corriente al suelo).

Sucesivamente mi amigo Jorge quiso desarrollar un trabajo que nos obligó a recordar y reestudiar los conceptos de campos magnéticos, y retomamos ordenadamente el estudio de campos, revisando bibliografía, mejorando el citado programa y agregando otros más en la colección.

Este apunte tiene el objeto de ayudar en el uso de algunos de estos programas, lograr aprovechar al máximo de ellos, y entusiasmar al alumno en el estudio de estos problemas que son mucho más importantes de lo que nos parece…

Resuelve la determinación del potencial en un punto en base al método de superposición, se obtiene el potencial en cada punto del espacio, sumando los potenciales debidos a cada una de las cargas consideradas en el problema, el programa guía proponiendo acciones a ejecutar,

1 - CAMBIA NOMBRES DE ARCHIVOS DE DATOS Y RESULTADOS, se definen o cambian los nombres de los archivos de datos y resultados.

2 - LEE EJEMPLO INTERNO, contenido en el programa.

3 - LEE ARCHIVO DE DATOS: cuyo nombre se ha indicado.

4 - PREPARA DATOS VALOR POR VALOR, permite prepararlos introduciéndolos todos uno a uno

5 - DEFINE TIPO DE PROBLEMA BIDIMENSIONAL O TRIDIMENSIONAL: se pueden proponer problemas bidimensionales (cilíndricos en el espacio, viéndose círculos en un plano), o tridimensionales (esferas en el espacio, pero con una limitación importante se trata de esferas cuyos centros están contenidos en un plano, y al observar el plano que pasa por los centros también se ven círculos en un plano, y este es el único plano que el programa reconoce).

6 - CALCULA Y GENERA ARCHIVO DE SALIDA GRAFICO: calcula el potencial en una cuadrícula espacial definida al inicio del lote de datos.

7 - EJECUTAR GRAFICADOR: ISOLUX Y LEVANTAR: ejecuta el programa de graficación (ISOLUX que a su vez propone nuevas acciones, el primer paso es informar correctamente el nombre del archivo de resultados - que se transmite con ISOLUX.SET - de POTESF, que son ahora datos de ISOLUX)

8 - GUARDAR ARCHIVO DE SETEO: ISOLUX.SET (SI NECESARIO)

9 - GUARDA DATOS: permite archivar los datos, que tambien se ecuentran al inicio del lote de resultados

0 - SALIDA

Los ejemplos preparados, y que pueden ejecutarse son los siguientes, y se propone ejecutarlos en opciones bidimensional (cilindros) y tridimensional (esferas).

POTESF1.DAT representa dos esferas (o dos cilindros) con cargas opuestas

POTESF2.DAT representa dos esferas (o dos cilindros) con cargas iguales

POTESF3.DAT representa cuatro esferas (o cuatro cilindros) al recorrer las cargas ordenadamente los signos cambian cada vez que se pasa de una carga a otra.

POTESF4.DAT representa cuatro esferas (o cuatro cilindros) con cargas iguales de a pares, dos cargas positivas y dos negativas al pasar de una carga a otra.

POTESF5.DAT representa cuatro esferas (o cuatro cilindros - un haz de cables) con cargas iguales

Se han preparado algunos gráficos que se muestran

Se propone observar y comparar esta figura, con la siguiente, notando que en proximidad de los círculos de radio unitario (no dibujados) el campo es más intenso cuando representan una esfera, ambas figuras se obtienen de POTESF1.DAT.

Sobre esta figura obtenida de POTESF5.DAT también conviene representar los círculos que corresponden al corte de los conductores. Este problema es conveniente resolverlo con una cuadrícula más densa, pudiéndose observar mucho mejor las líneas equipotenciales POTESFC.DAT.

Físicamente la superficie de reflexión se comporta como una pared metálica (en la cual las líneas de campo son normales).

El método puede ser usado para varias cargas próximas a una pared metálica o al suelo conductor (simplemente de elevada conductividad respecto del espacio dieléctrico).

Supongamos que se tiene una carga eléctrica en un conductor sobre el suelo, la superficie del suelo es la superficie de reflexión, se reemplaza el suelo por espacio libre y se pone una carga imagen (igual y contraria).

Si además hay una pared se tienen dos superficies normales de reflexión si la carga es + habrá dos imágenes - (de reflexión en cada pared) y otra imagen + (de segunda reflexión, en la pared reflejada).

Si la carga esta entre dos paredes paralelas entonces las imágenes son múltiples (en teoría infinitas imágenes) a medida que las imágenes están alejadas su influencia en el área de interés disminuye, efectivamente, las cargas muy alejadas de un punto tienen poca influencia en el punto.

Analicemos una carga encerrada con piso, paredes y techo, cuatro superficies de reflexión, debemos lograr identificar todas las imágenes, que podemos imaginar como sucesivas capas.

Surge natural otra pregunta, y si la superficie fuera curva? Es valido pensar en un espejo curvo? Este problema se presenta cuando se observa un conductor dentro de un tubo metálico excéntrico, o al plantear el campo en el espacio dieléctrico entre dos esferas (espinterometro de esferas).

Las ideas planteadas deben profundizarse, el método permite resolver gran cantidad de problemas que observamos alrededor nuestro.

La explicación que sigue está ligada al programa POTRES, que resuelve numéricamente ecuaciones diferenciales (bidimensionales) en derivadas parciales. El método aplicado es llamado de diferencias finitas, el espacio se divide con una cuadrícula, y para cada punto se plantea una ecuación en diferencias obtenida de realizar una aproximación de la ecuación diferencial.

Las ecuaciones planteadas son de distintos tipos, según el punto se encuentre dentro de un material (uniforme), en un límite entre dos materiales, contra una equipotencial, contra una línea de campo (normal a las equipontenciales). Estos algoritmos están contenidos en el programa, y son llamados para resolver el problema. En rigor la determinación del potencial se hace en un área y en base a un método de relajación, punto por punto iterativamente se aplica el algoritmo que corresponde y lentamente se mejora la solución.

El programa guía proponiendo las acciones a ejecutar,

1- Definir el tamaño del área de estudio (la cuadricula, máximo 50)

2 - Informar nombres de archivos de datos y resultados.

3 - Preparación del archivo de datos.

4 - Editar el archivo de datos, para cambiar o corregir.

5 - Selecciona el método de cálculo (relajación o sobrerelajación)

6 - Calcula y genera un archivo de salida apto para graficar

7 - Genera una tabla de resultados que muestra en forma aceptable el potencial en cada punto de la cuadrícula.

8 - Convierte el archivo de datos en un archivo dual, para poder determinar las líneas de campo como equipotenciales (esta opción requiere retoques hechos con el editor).

9 - Ejecutar el graficador ISOLUX

10 - Archivar el seteo de los datos (archivo ISOLUX.SET)

11 - graficar con POTDIB los limites del problema.

Una observación importante es que cuando los datos se observan con el editor, el eje Y es horizontal de izquierda a derecha, y el eje X va de arriba hacia abajo, cuando en cambio se obtiene el gráfico, este tiene los ejes convencionalmente dispuestos, X de izquierda a derecha Y de abajo hacia arriba.

El editor muestra un rectángulo lleno de caracteres que representan puntos. Cada punto del rectángulo corresponde a una letra o un número cuyo significado se indica:

0, 1 a Q potencial, línea equipotencial valor 0, 10 a 100

V el potencial intermedio entre 0 y Q, se interpola al momento del cálculo

E punto externo al campo, no se calcula

I punto interno al campo, se calcula con puntos N S E W

X punto interno al campo, dentro de material e

L punto límite entre los dos materiales 1 y e

J punto interno de bobina, al menos debe haber 4 puntos J se calcula como I

C o D línea de corriente, el punto E se hace igual al I

Varios lotes de datos permiten realizar distintos casos que merecen ser analizados como ejemplos, el programa trabaja resolviendo el problema plano, y el caso de simetría cilíndrica, este ultimo requiere definir el radio r0 que si es muy pequeño corresponde al eje del cilindro, si en cambio es grande (mas de 0.5) es un núcleo dentro del cuerpo en el que se estudia el campo.

POTRES1.DAT Terminal cable sin botella (ejecutarlo con radio 3 para ver la influencia de la simetría cilíndrica)

POTRES2.DAT Terminal cable con cono (ejecutarlo también con radio 3)

POTRES3.DAT Terminal cable con cono metálico (ejecutarlo también con radio 3)

POTRES4.DAT Pasatapas (ejecutarlo también con radio 3)

POTRES5.DAT Pasatapas con polleras (ejecutarlo también con radio 3)

POTRES6.DAT Aislador soporte (ejecutarlo también con radio 0.001)

POTRES7.DAT Aislador soporte con pantalla (ejecutarlo también con radio 0.001)

POTRES8.DAT Burbuja dentro del dieléctrico (el lote de datos solo tiene sentido para el caso plano)

POTRES9.DAT Burbuja dentro del dieléctrico, contra una placa (solo valido para plano)

AISLADOR.DAT Aislador suspensión (ejecutarlo también con radio 0.001)

TAT5V.DAT Bobina transformador

TAT6V.DAT Cabeza bobina alternador (2 dieléctricos)

TAT7V-DAT Varilla - plano (ejecutarlo también con radio 0.001)

Se han preparado distintos casos, a partir de POTRES1.DAT se obtuvo:

Obsérvese el campo máximo en la proximidad de la terminación de la pantalla electrostática (a potencial nulo) y compárese con el campo en la finalización de la pantalla superpuesta al cono del lado cable obtenido a parir de POTRES3.DAT:

En los aisladores pasamuros se observa que el campo es intenso en el área en la que efectivamente se atraviesa la chapa (POTRES4.DAT). Es interesante el experimento de prolongar el aislador, observando que el campo en la zona de atravesamiento no cambia, por lo tanto un aislador de mayor tensión no puede fabricarse prolongando uno de menor tensión simplemente...

Los aisladores soporte deben generar en lo posible un campo uniforme, parecido al que se tendría sin su presencia... experiméntese modificando el lote de datos de POTRES6.DAT, obsérvese la influencia de las polleras (conos) del aislador.

Pequeñas irregularidades dentro del dieléctrico uniforme son causa de concentraciones de campo, que aumentan la solicitación dieléctrica de los materiales e inician procesos de falla (descargas). POTRES9.DAT muestra el caso de una burbuja de gas dentro de un dieléctrico, y a partir de este caso se pueden plantear otros similares (por ejemplo, una gota de agua, o una bolita de metal dentro del dieléctrico gaseoso).

Hemos visto que para conocer el campo en un punto se utilizan programas desarrollados con este objetivo, sin entrar en detalles parece conveniente explicar como las ecuaciones en derivadas parciales de la física se han transformado en ecuaciones algebraicas para finalmente convertirse en algoritmos de cálculo numérico. No es objeto de esta guía la programación, pero alrededor de este tema parece importante poner en evidencia como se encara el trabajo, esto ayudará a entender el por que de una presentación de datos que se puede considerar capciosa.

La explicación que sigue está ligada al programa POTRES. Pero los conceptos que se exponen quizás contribuirán a mejorar la comprensión cuando se esté frente a poderosos programas comerciales desarrollados para resolver mejor estos mismos problemas. Observemos un punto X rodeado de cuatro puntos en direcciones N, S, E, O, la integral sobre el camino (superficie) que rodea al punto X es:

Si e es igual y constante esto equivale a:

Si e varía entonces debe hacerse:

Veamos primero el caso de medio homogéneo y que tenga espesor constante (problema plano, independiente de z), el camino S esta formado por cuatro lados dS de un pequeño cuadrado, reemplazando la integral por la suma de valores en los elementos que rodean el punto X (siendo e igual en todos los puntos):

Reemplazando los valores de E por la diferencia entre potenciales de los puntos extremos, y eliminando el factor común dS se tiene:

Que permite determinar una mejor aproximación de V_X a partir de los valores de V que rodean el punto X

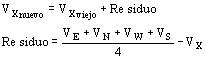
Esto es lo que se hace para resolver el problema en un punto... Cuando el medio no es homogéneo (pero el problema sigue siendo plano), y se tienen dos dieléctricos de distinto e a ambos lados de una línea que pasa por X la ecuación debe tener en cuenta los valores de e . Supongamos que hay un e _N y un e _S, entonces debemos resolver:

En algunos tramos del camino el e es constante, en otros tiene dos valores por lo que el camino debe dividirse en dos tramos

Reemplazando los valores de E por la diferencia entre potenciales de los puntos extremos, y eliminando el factor común dS se tiene:

ahora las diferencias de potenciales están ponderadas con un factor que según en que región nos encontremos vale e _N, e _S o el valor medio, determinamos el residuo como en el caso anterior:

Observemos que los potenciales están afectados por un factor de peso que vale e _M cuando el punto esta en la frontera, y e _N o e _S si el punto esta en el medio donde homogéneo, a medida que se rodea el punto se hace la suma de V_i ´ e _i, y la suma de e _i, y luego la relación entre estas sumas es la que se usa para calcular el residuo.

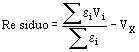
La frontera ha pasado por E, X, O, la regla es igual cualquiera sea la frontera, considérese N, X, O o en diagonal NE, X, SO por ejemplo, lo único que debe cuidarse es usar los e adecuados según el punto este sumergido en un medio, en el otro o sea frontera. Si e _N y e _S son iguales se vuelve a la ecuación válida para medio homogéneo que vimos primero. Si el punto X no es frontera entre ambos medios el e es único, el medio es homogéneo.

Una gran cantidad de problemas presentan simetría cilíndrica, en este caso también puede plantearse un plano que pasa por el eje del cilindro, y que se divide con una cuadricula uniforme, también este problema puede incluir dos medios dieléctricos, las ecuaciones en elementos finitos son un poco mas complicadas.

Si el punto pertenece al eje (por razones de simetría) el medio es único, solo puede cambiar en el sentido del eje del cilindro. Si en cambio el punto esta alejado del eje, el cambio de medio puede presentarse como antes visto para el plano. Habiendo simetría cilíndrica, y dos medios dieléctricos, con ejes r y z, y siendo dr = dz, se plantean las ecuaciones de la siguiente forma:

separamos las variables obteniendo:

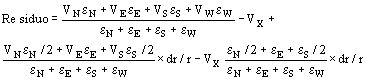
Esas formulas corresponden al caso en que r > 0, si se debe trabajar en puntos donde r = 0 entonces las formulas a aplicar son:

El valor del residuo obtenido en estos casos se puede comparar con el valor definido para el caso del problema plano, especialmente para el, caso de r > 0 se observa aparece un ulterior termino, que puede interpretarse como un factor de corrección y que depende de dr / r, reduciéndose la influencia de este factor a medida que r aumenta.

El programa POTRES hace reiteradamente esta operación en todos los puntos de potencial desconocido, y así mejora la aproximación.

Hay algunos puntos especiales, de borde (frontera):

Los puntos con potencial conocido no se calculan porque precisamente su potencial es conocido.

Los puntos límite del campo en los cuales la línea de campo es precisamente el límite se pueden resolver agregando un punto fuera del campo que es imagen del interior respecto de la frontera.

De esta manera recorriendo todos los puntos, se determina el residuo en cada punto, y a partir de el obtiene un potencial mejor en cada punto.

El cálculo de los potenciales nuevos se puede hacer una vez calculados todos los residuos, o bien a medida que se calcula un residuo corregir el potencial del punto, en este último caso las correcciones tiene efecto inmediato y el resultado se alcanza más rápido.

El proceso también puede acelerarse con un factor alfa que aumenta el peso del residuo en la corrección, factor de aceleración, esto explica algo más algunos carteles que el programa muestra para guiar en el uso.

Es el uso del programa el que nos va a generar la experiencia, sabremos usarlo, y lograremos la experiencia en los efectos de los campos, el esfuerzo de usar los programas vale la pena.

Todos los ejemplos desarrollados muestran líneas (superficies pensando en tres dimensiones) equipotenciales, si nos interesan las líneas de campo deberíamos construir perpendiculares a las equipotenciales.

Como las familias de equipotenciales y las líneas de campo son perpendiculares entre si, podemos pensar que si cambiamos los significados de los limites de nuestro problema, a las equipotenciales limites las convertimos en líneas de campo, y las líneas de campo limites las hacemos equipotenciales, la solución de este nuevo problema nos mostrara nuevas equipotenciales que son las líneas de campo del problema primitivo.

Este es un criterio de analogia que frecuentemente se utiliza para resolver problemas de este tipo. Una opcion de POTRES genera un archivo dual, reemplazando los valores de contorno equipotenciales del campo, por lineas de campo, y lineas de campo por equipotenciales, hecho esto se debe generalmente ajustar el lote de datos adecuándolos a para que el objeto dual sea mas correcto.

Esta analogía es valida también cuando el campo contiene medios dieléctricos distintos, presentamos a continuación el ejemplo de la burbuja de aire dentro de un dieléctrico,

Estas figuras surgieron a partir del lote BURBUJA.DAT, que fue convertido en BURBUJB.DAT con la opción 8 de POTRES, que convierte el archivo de datos en un archivo dual, cuyas equipotenciales son las líneas de campo del lote de datos original (obsérvese que después del procesamiento de POTRES se tuvo que manipular ligeramente en lote agregando la equipotencial 0 en el eje de simetría, y prolongando la equipotencial Q a los limites del área)

Las figuras se obtuvieron para un caso de radio = 0.001 observándose la simetría de rotación, y en este caso la analogía no corresponde a cuadrados curvilíneos como para el caso de simetría plana, se propone desarrollar un ejemplo correspondiente a un caso plano y explicar las razones de las diferencias.

Ya se ha citado el programa ISOLUX, que es llamado para graficar las líneas equipotenciales que corresponden a POTRES y de POTESF, el graficador toma cada cuadrado de la retícula, y a partir del conocimiento que tiene del potencial en los cuatro vértices traza rectas equipotenciales por interpolación.

Si la cuadrícula es grande se observan las líneas equipotenciales quebradas, si se hace densa las líneas equipotenciales son apreciadas como líneas curvas y continuas.

Es aconsejable preparar los problemas para su análisis con baja densidad de puntos, y solo cuando se quiere afinar el cálculo, u obtener una figura hermosa aumentar la densidad al máximo posible.

Otro programa POTDIB gráfica los datos de POTRES, y es útil para verificar la forma del objeto de cálculo, se observan las líneas equipotenciales de 0 y 100% (líneas 0 y Q), y la línea de separación entre medios dieléctricos (L), estos puntos aparecen en la retícula con colores convencionales blanco (0), rojo (Q), y verde (L).

POTESF durante la ejecución llama a ISOLUX, y los nombres de los archivos involucrados se transmiten mediante ISOLUX.SET, que es generado por POTESF.

También POTRES llama a ISOLUX o a POTDIB, y los nombres de los archivos involucrados se transmiten mediante ISOLUX.SET, que es generado por POTRES.

Esperamos que este apunte cumpla su objetivo, que es mostrar lo interesante que es conocer los campos eléctricos (algunos casos se han planteado) permitiendo obtener imágenes que muestran como varían los potenciales debidos a las distintas condiciones que se presentan.

Por analogía se pueden explorar campos magnéticos, campos térmicos, campos de fuerzas, flujos de fluidos, y otros problemas que deben encararse desde este ángulo y que mucho interesan en el ejercicio de la profesión para explicar fenómenos que ocurren.

Seguramente quienes avancen por este camino deberán utilizar mejores programas, pero con costos que no son alcanzables cuando se trata simplemente de resolver problemas con finalidad didáctica, o satisfacer modestas curiosidades técnicas.

Algunos al estudiar seguramente querrán interesarse más por como los programas desarrollan su trabajo, los programas presentados están hechos en QBASIC, dicho esto si la curiosidad no se ha inhibido le proponemos intente contactarnos que con tiempo podremos intercambiar opiniones sobre este trabajo...

Es deber agradecer a Beatriz (Betty) que mucho ayudo a plantear los modelos con dieléctricos, y los modelos con simetría cilíndrica, sin los cuales el programa casi no tendría utilidad practica.