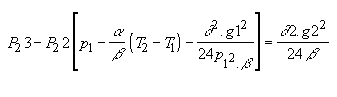
V. CALCULO DE LA TENSION MECANICA DE UN CONDUCTOR PARA UNA CONDICION CUALQUIERA PARTIENDO DEL ESTADO BASICO.
Recordaremos la ecuación de cambio de estado del conductor:
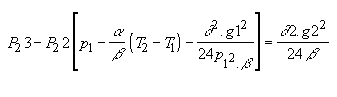
Mediante el empleo del concepto de vano crítico y las técnicas de resolución explicadas se determina el estado básico, por ejemplo el estado I, al cual le asignamos la Padm.
Luego mediante el uso de la ecuación de cambio, que en forma simplificada se puede escribir como:
![]()
Que es la expresión de un ecuación de tercer grado en grado Pz, se puede determinar la tensión mecánica del otro estado. A partir de la misma y recordando que:
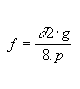
se puede calcular la flecha correspondiente a dicho estado.
VI. CALCULO MECANICO DEL CABLE DE GUARDIA
El cálculo mecánico se repite para el cable de guardia. Puede suceder que, dado que la sección y material del mismo son diferentes al del conductor, que los vanos críticos sean diferentes y, quizás, el estado básico resulte distinto.
dado que el conductor debe ser protegido por el cable de guardia, hay que verificar que la distancia C2, en el medio del vano, sea mayor que la distancia de separación existente en el poste C. (Ver figura 6)
Para que ello ocurra se calcula el cable de guardia verificando que se cumpla para todos los estados de carga que:
![]()
Para ello se procede de la siguiente manera:
Se adopta una tensión máxima admisible, considerando que las tensiones de rotura usuales para cables de guardia se pueden elegir entre 60 y 120 Kg/mm2.
Se calculan los vanos críticos.
Se determina el estado básico.
Se realiza el cálculo mecánico.
Se verifica la relación de flechas entre el cable de guardia y el conductor.
De no verificarse, se calcula con la flecha del conductor de dicho estado la nueva tensión mecánica p, con la expresión:
![]()
Con la nueva tensión mecánica se reinicia el cálculo, a partir del segundo paso.
Así sucesivamente hasta obtener que se cumpla la relación de flechas.
NOTA: Algunos proyectistas consideran que fcg £ 0,9. fcond solo se debe verificar en el estado de aplicación de la temperatura media anual, cuyo significado se discutirá posteriormente.
VII. GENERALIZACION PARA APOYO A DISTINTO NIVEL.
A menudo se presenta el caso de que los dos puntos fijos de suspensión de la cuerda
están a distinto niveles, siendo la diferencia ![]() entre ambos puntos (ver figura 7).
entre ambos puntos (ver figura 7).
Resulta así que prolongando el arco d la parábola (o catenaria), desde el punto A hasta el C que se encuentra al mismo nivel de B, estaremos en presencia del arco CADB, que es el estudiado anteriormente, correspondiente a un vano ficticio a1. Bajo estas condiciones se tiene la flecha ficticia f,
la cual puede estar ubicada a la izquierda del punto D, en el punto D, o a la derecha del punto D, todo depende donde esté ubicado el punto A.
Los tres casos están representados en la figura 8
El valor de a1 se obtiene
![]()
La flecha f como.
![]()
y los valores de m y n
![]()
![]()
además
![]()
siendo az la distancia entre A y B (ver
figura 9). Para desniveles no muy grandes se puede expresar que![]()
además como
![]()
de donde
![]()
reemplazando
![]()
NOTA: Para una mayor información sobre el tema ver "Líneas de Transporte de Energía", autor: Checa, o el artículo del Ing. Rezzonico de la revista Electrotecnia de Marzo-Abril de 1986, pag. 73, 76.
CARGAS Y FUERZAS ACTUANTES
I. Sobre el conductor
Según hemos visto anteriormente el conductor esta sometido a cargas específicas debidas al peso propio, al viento al hielo. A continuación se desarrolla la respectiva metodología de cálculo.
1) Peso propio
La carga específica debida al peso propio se determina según la siguiente ecuación.
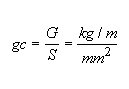
siendo G: peso propio del conductor (dato del fabricante).
S: sección real del conductor (dato del fabricante o por cálculo).
2) Viento
Para calcular la carga específica debida al viento partimos de considerar un viento de velocidad y actuando sobre una placa; el mismo ejercerá sobre ella una presión p. Utilizando la fórmula de Bernoulli:
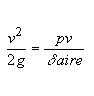
siendo v: velocidad del viento, m/seg.
d : peso específico del aire = 1,29 Kg/dm3.
g: aceleración de la gravedad = 9,81 m/seg2
figura 10 en consecuencia: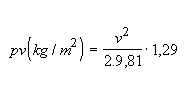
en donde
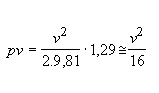
La carga del viento sobre un conductor cilíndrico (
figura 11) se afecta de un coeficiente de presión dinámica C (ver tabla I) que depende de la forma del elemento, ya que la ecuación deducida es válida para placas planas; y de un factor k, que toma en cuenta la desigual acción del viento a lo largo del vano.k: 0,75 - 0,80 para cables
k: 1 para el resto de los elementos
pv = C . k. v2/16
y la fuerza del viento será:
F = pv. Superficie
F = C . k (v2 / 16) a. dc
siendo dc : diámetro del conductor, en m2
a: longitud del vano.
Finalmente la carga específica será:
![]()
siendo S: sección real del conductor, mm2
Nota: recordando la
figura 4, obsérvese que con carga de viento la flecha no aparece mas en el plano vertical. Prácticamente se puede ver que con un viento de 120 Km/h un conductor de Al/Ac de 70/12 se inclina ángulo del orden de los 70 grados.3) Hielo
Es una carga específica de zonas de muy baja temperatura. El calculo es aproximado. Se toma un valor razonable en base a los registros meteorológicos.
Por otra parte se admite que el hielo forma un manguito cilíndrico (ver
figura 12) alrededor del conductor (cosa que en realidad pocas veces ocurre).rc = radio del conductor Calculo de la sección
R = radio con manguito de hielo
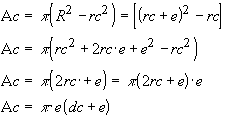
e = espesor del manguito
d h = 0,95 Kg/dm3
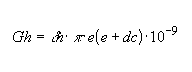
Luego la carga especifica será
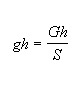
siendo S: sección real del conductor
La presencia del manguito de hielo no solo incrementa el peso sino también de existir viento en dicha condición climática, aumenta la superficie expuesta al mismo y consecuentemente la solicitación gv.
Las
Tablas III, IV, V dan el calculo de gc, gh, gy, y gtotal para cobre, aluminio con alma de acero y aleación de aluminio para distintas secciones y velocidades de viento.II. Sobre aisladores
a) peso propio
El peso propi del aislador es dato del fabricante.
b) Fuerza del viento
Los aisladores no están en cuadrados dentro de una superficie sencilla, entonces se debe adaptarlos. La superficie normal es un triángulo (ver
figura 13) de aproximadamente 254.150 (para aisladores de suspensión, de campana normal) entonces Fva.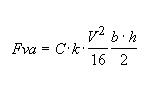
La mayor dificultad consiste en determinar los coeficientes C y K. Para vientos de 130 km/h se adopta Fva = 1,4 kg / aislador.
III. Sobre la estructura
I. Postes
1a. Peso propio
El peso propio de los postes de hormigón o de acero es dato del fabricante; en el caso de estructuras reticuladas se debe calcular.
1b. Fuerza del viento
Los postes de hormigón o los tubos trococonicos de acero tiene la forma trapezoidal que muestra la
figura 14.La fuerza del viento estará aplicada a la altura del centro de gravedad de la superficie del mismo. Para ello calcularemos la paralelogramo:
Reemplazando las superficies por sus valores:
![]()
de donde la altura del centro de gravedad de la superficie del paralelogramo resulta:
![]()
Interesa establecer la fuerza del viento sobre el poste referida a la cima.
F.hp.=presión del viento x.sup expuesta x . altura centro de gravedad.
![]()
donde C y K corresponden al poste utilizado.
En definitiva
![]()
Esta ecuación es válida para postes simples, para el caso de otros estructuras se emplean los valores de
figura 15.2. Vínculos
Se emplean para unir las estructuras de mas de un poste, el criterio de ubicación espesor de los mismos ya ha sido discutido.
2a. Peso propio
En forma aproximada se toma 2200 kg / m3
2b. Fuerza del viento
Vease la
figura 16, donde se incluye:L = s + (dp + 0,10)
siendo dp : diametro del poste a la altura del vinculo
dp = dcima = 0,015 (dist . cima dist. vinculo
s : separación cima + separación a la altura del vinc)
s = 0,3 + 0,04 (dist . cima dist. vincul.)
Una vez calculada la fuerza vincul. del viento, debe ser referida a la cima, mediante la expresión.
![]()
3. Mensula
3a. Peso propio
En forma aproximada se toma como 2200 Kg/m3.
3b. Fuerza del viento
Observese la
figura 17, :![]()
siendo A: superficie expuesta al viento.
Una vez determinada la fuerza del viento, debe ser referida a la cima mediante la expresión.
![]()